Altın dikdörtgen, uzun kenarının kısa kenara oranı 1.618 olan özel bir dikdörtgendir. Bu benzersiz oran, altın oran (Φ) olarak da bilinir. Şimdi, bu simülasyonla altın dikdörtgeni nasıl oluşturabileceğinizi keşfedin! Kırmızı dikdörtgenin bir kenarının uzunluğunu değiştirerek tüm dikdörtgenin altın oranı yakalamasını sağlayın!
Lise matematik öğrencisiyseniz matematik müfredatında eşdeğer kesirler, diferansiyel denklemler, cebir, geometri, trigonometri, olasılık, Pisagor teoremi ve diğer önemli matematiksel kavramları duymuş ve öğrenmişsinizdir.
Ancak bu bilgilerin okul öncesi ve ilkokuldan beri size öğretilen matematik temelleri üzerine inşa edildiğini fark etmeyebilirsiniz. Toplama ve çıkarma, çarpma ve bölme, tüm matematik konularını anlamanın temelleridir ve bu matematik problemlerini kavrama ve çözme yeteneğiniz, sizi şimdi matematikte ustalık yolunda yönlendiren şeydir.
Matematiği öğrenme konusunda ciddiyseniz diziler, kesirler ve cebirsel matematik kavramları görmüşsünüzdür. Ayrıca matematiğin sadece tipik tam sayılardan değil, aynı zamanda sayı sisteminin farklı bölümlerini temsil eden semboller ve harflerden oluştuğunu da fark etmiş olabilirsiniz.

Bu özel sayılardan bazıları pi, Euler sayısı e, özel sayı i ve tabii ki altın orandır.
Müfredatın çarpım tablosu, toplama ve çıkarma olduğu ilkokul matematik sınıfından çıktıktan sonra matematik dünyasına açılmaya başlarsınız. Matematik, bugün toplumumuzun birçok kesimi için ortak temel standartlardan biri olduğundan konuyla ilgili bilginizi tamamlamanız büyük bir beceridir.
Matematik, sayı kalıpları ve matematiksel modeller hakkında daha fazlasını öğrenmek için altın orana bir göz atacağız.

Altın Oran Nedir?
Altın oran nedir matematik disiplininde önemli bir sorudur. İlahi oran veya altın oranın doğada doğal olarak meydana gelen mükemmel oran olduğu söylenir.
Matematikte iki miktardan büyük olanın küçüğe oranı, miktarların toplamının miktarların büyük olanına oranı ile aynı ise altın orandır.
a+b/a = a/b = 1.618034
İki uzunluğun a + b toplamının en büyüğüne oranı, en büyüğün en küçüğüne oranıdır.
Altın oranın cebirsel gösterimi ise aşağıdaki gibidir:
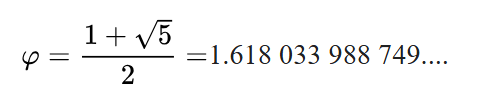
En üstteki simülasyon örneğinden gidelim! Oluşturduğumuz dikdörtgenin;
- Uzun kenarı 100+61.8 = 161.8 piksel
- Kısa kenarı ise değişmiyor, 100 piksel
Dolayısıyla 161.8px / 100px = 1.618 oranını yakalıyoruz!
Gördüğünüz gibi matematiksel modelin karekök veya alan ve hacim ile ilgisi yok. Bu altın oran olarak sınıflandırılır çünkü uzun kenarı (161.8 piksel) kısa kenara (100 piksel) böleriz, bu bize cevabımızı verir ve cevap altın oran dizisiyle eşleşir. Altın oranın kesre dönüştürülemeyeceğini ve ondalıklarının sonsuza kadar devam ettiğini, bunun da onu irrasyonel bir sayı yaptığını bilmek de önemlidir.
Asal sayılara da göz atmayı unutmayın!
Matematikçiler ve Altın Oranın Tarihi
Sıfır sayısı hakkında daha çok şey öğrenmeye ne dersiniz?
Matematikçi Fibonacci'ye Yakından Bakış
Altın oran kavramını geniş kitlelere tanıtan kişi olarak Fibonacci, bu alandaki en önemli isimlerden biri olarak kabul edilir. Ancak, Fibonacci adıyla tanıdığımız bu ünlü matematikçinin gerçek adının Leonardo Pisano olduğunu biliyor muydunuz?
Leonardo Pisano ve Fibonacci Adı
Leonardo, 12. yüzyılın sonlarında İtalya’nın Pisa kentinde doğdu. "Fibonacci" adı ise aslında daha sonra türemiş bir unvandır. "Filius Bonacci" (Bonaccio’nun oğlu) ifadesinden gelen bu isim, Liber Abaci adlı kitabının el yazması kopyalarındaki bir yanlış anlamadan doğmuştur. Böylece Leonardo, yüzyıllar boyunca Fibonacci olarak anılmaya başlandı.
Fibonacci Dizisi ve Altın Oran
Fibonacci, günümüzde en çok, adını taşıyan ünlü sayı dizisiyle bilinir: 0, 1, 1, 2, 3, 5, 8, 13, ... Bu dizideki ardışık sayıların birbirine oranı, altın orana giderek yaklaşır. Fibonacci, Liber Abaci'yi, özellikle o zamanlar farklı para ve ağırlık sistemlerine sahip küçük kasaba ve bölgelerden oluşan İtalya'da, ticari ilişkilerinde birçok pratik sorunu olan tüccarları bilgilendirmek için yazdı. Mevcut Romen rakamlarına kıyasla bu yeni sayı sistemiyle hesaplamaların ne kadar basit yapılabileceğini gösteren örnekler verdi.
Matematik özel ders Ankara seçeneklerinizi öğrenmek için linke tıklayabilirsiniz.


Altın Oranın Kullanım Alanları
- Plato, Parthenon'u tasarlamak için kullandı
- Mısırlılar piramitleri tasarlamak ve inşa etmek için kullandılar.
- Mimari: Notre Dame, Tac Mahal ve Kairouan Ulu Camii'nin tümü altın orana sahiptir.
- Sanatçılar: Da Vinci, Dali ve diğerleri, eserlerinin düzeninde altın oranı sürekli kullandılar.
- Müzik: Bach, Debussy, Beethoven ve Chopin'in müziklerinde de altın oran tespit edilebilir.
- Kitaplar: İncil altın oran sayı sisteminden ve orana göre inşa edilen şeylerden bahseder
- Doğa: Çiçekler, bitkiler, yiyecekler ve daha fazlası altın orana uygun olarak büyür. Kasırgalar ve kaosu bile altın oranların sayı doğrularını takip eder.
- Hayat: Böcekler, hayvanlar ve insanların altın oran ile bir bağlantısı vardır. Da Vincis
- Vitruvius Adamı çizimine baktığınızda, insan vücudunun altın orana göre yaratıldığını görebilirsiniz. Günümüzde psikologlar, altın orana uygun özelliklere sahip olanların insanlara daha çekici geldiğini belirtmişlerdir. Altın oran DNA'mızda bile görülebiliyor.
- Estetik cerrahların, hastaların yeni görünümünü planlamak için bu altın orana dayalı bir 'phi mask' kullandığını biliyor muydunuz? Buna gerçekten "matematiğin güzelliği" diyebiliriz!
Mükemmel sayılarla ilgili daha çok şey öğrenmek için makalemizi okuyun.
Altın Oran Neden Kullanılır?
Altın Oran, her yerde görülebilen, gerçekten büyüleyici bir sayıdır. DNA'mızın yapı taşları bile bu prensibi takip eder. Sizce de büyüleyici değil mi? Bu üstel sayı, bir şekilde evrenin her köşesine nüfuz etmiştir. Galaksilerden arılara, çiçeklerden havaya.
Altın ilke, mantığı nedeniyle bana çok ilginç geliyor. İrrasyonel bir sayı olmasına rağmen bu dizinin bize sunacağı çok şey olması su götürmez bir gerçek. Bu oranı bir matematik problemi çözerken kullanabilirsiniz. Estetik açıdan hoş bir şey tasarlamanıza yardımcı olması için kullanabilirsiniz. Hatta biraz eğlenceli şeyler için kullanabilir ve altın oranı evinizde, hatta kendi yüzünüzde keşfedebilirsiniz.
Bunu anaokulunda veya ilkokul düzeyinde öğretildiğini göremeyebilirsiniz ancak belki de lise matematik sınıfında bu orana yer verilebilir. Bu matematik, bilim, felsefe, gerçeklik ve keşfin sınırlarında var olan eğlenceli bir matematiktir. Bu, lineer denklemler, diferansiyel denklemler, polinom üçgenler veya diğer matematiksel kavramlara hâkim olmaya benzemez.
Gerçekten de lisede matematik dersleri bile eğlenceli ve heyecan verici olabilir. Bu teorem hâlâ keşfediliyor ve araştırılıyor, bu yüzden adınızı tarih kitaplarına yazmak istiyorsanız altın oran, asil bir ödül kazanma fırsatınız olabilir!
Matematik öğrenen biri olarak altın oran hakkında bilgi edinmek, matematik becerileri listenize eklenmelidir. Ancak temelinizin (aritmetik, çıkarma, çarpma problemleri vs.) iyi olduğundan emin olun. Çünkü size daha karmaşık konuları anlamanız ve üzerinde çalışmanız için güçlü bir temel oluşturur.
Bir Öğretmenle Matematik Öğrenin
Matematik kolay bir ders değildir ve bu nedenle üzerinde çalışamayacağınız bir alanla karşılaşırsanız kendi başınıza çalışmak çok zor olabilir.
Bir öğretmen, belli bir noktada takılıp kalmamanız için zor bulduğunuz kavramları açıklayarak size yardımcı olabilir. Çünkü matematiğin büyük bir çoğunluğunda başka bir kavramda ilerleyebilmeniz, belli bir kavramı anlamanıza bağlıdır.

Bire bir eğitim için kendinize bir özel matematik öğretmeni bulun. Kütüphanelerde ve gazetelerde reklam veren öğretmenleri arayabilir veya yakınınızdaki bir öğretmeni bulmak için Superprof gibi online bir platformu kullanabilirsiniz.
Özel Ders Öğretmeni
Özel bir matematik öğretmenine sahip olmanın avantajı, öğretmeninizin tam dikkatine sahip olmanız ve dersleri ihtiyaçlarınıza göre uyarlayabilmeleridir. Yani zayıf olduğunuz bir nokta varsa öğretmeniniz derslerinizde ve ödevlerinizde buna odaklanabilir.
Eğitmenlerin ve öğrencilerin bağlantı kurmaları ve beraber çalışmaları için lider bir platform olan Superprof, bölgenizde matematik özel ders hizmetleri sunan ve uzaktan online eğitim sunabilen öğretmenleri anında bulabileceğiniz kullanıcı dostu bir web sitesidir.
Superprof'taki 80.000'e yakın öğretmen, matematikle ilgili endişeleriniz konusunda size yüz yüze veya görüntülü arama yoluyla yardımcı olabilir. Saatte sadece 63 TL'den başlayan ücretlerle, ihtiyaçlarınızı karşılayabilecek ve matematik derslerinizde ilerlemenizi sağlayacak birini bulabilirsiniz. Kimisi matematikçi, kimisi nitelikli öğretmen, kimisi de sayılara hâkim, bilgi ve becerilerini aktarmak isteyen bireylerdir.
Yani eğer hâlâ altın oranı ve bu gibi özel kavramları anlamakta zorlanıyorsanız öğrenmek için öğretmen adaylarıyla iletişime geçin!
Yapay zekâ ile özetle
















