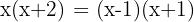Polinom soruları ve denklemler... Bu ikisi matematik sınavlarında karşınıza en çok çıkacak kavramlardandır. Bazı denklemlerde karşınıza bölme işlemleri de çıkacaktır. Yani kesirli denklemlerle karşılaşacaksınız. Bu durumda şunu hemen hatırlatalım:

Şimdi biraz da bu durumda matematik problemlerini nasıl çözebileceğimize bakalım. Bölme işlemli denklemleri çözerken yapacağınız en iyi şey, önce kesirden kurtulmak olacaktır. Bunlar size fazlasıyla karmaşık gelebilir. Ankara özel ders öğretmeni veya hangi şehirde yaşıyorsanız tecrübeli bir öğretmen ile daha kolay olacaktır.
Burada da denklemleri çözerken uyguladığımız yöntemi aynen uygulayacağız. Eşitliğin her iki tarafının da bize aynı sonucu vereceğini hatırlayın.
Hemen bir örnekle devam edelim:
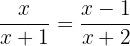
Bu ilk bakışta zor gelebilir ancak aslında çözümü çok kolay. Rasyonel sayılarla birlikte normal çözümlerde takip ettiğimiz adımları takip edeceğiz: x'i yalnız bırakacağız ve eşitliğin sonucunu sıfır bulacağız!
Az önce de dediğimiz gibi hiçbir şeyi sıfıra bölemeyiz. Bu nedenle paydalardan kurtulmaya çalışacağız.
Önce eşitliğin sol tarafındaki paydadan kurtulmakla başlayalım:
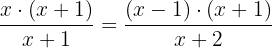
Doğrusal denklem örneğinde yaptığımız gibi her iki tarafı da (x+1) ile çarpacağız ki paydadan kurtulalım. Soldaki kesri (x+1) ile çarptığımızda payda ile birbirini götürecek. Böylece elimizde şöyle bir denklem kalacak:
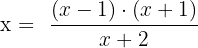
Artık x'i yalnız bıraktığımıza göre denklem daha kolay görünüyor, değil mi? Şimdi aynı yöntemi kullanarak sağdaki paydadan da kurtulalım:
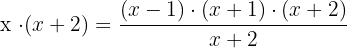
Bu noktada işleri daha da karıştırdık gibi görünüyor ama merak etmeyin, paydadan kurtulmak çok işimize yarayacak. Az önce sol tarafta yaptığımız gibi sağı da (x+2) ile çarptığımızda payda ile birbirini götürecek. Böylece bölme işleminden kurtulmuş olacağız.
Şimdi bu denklemi biraz daha basit göstermek için o çarpı işaretinden de kurtulalım. Denklemleri çözmeye başladıysanız zaten o işareti kullanmamız size garip gelmiştir!
Gördüğünüz gibi, bu denklem daha düzenli ve anlaşılır hale geldi. Artık yalnızca xxx ile ilgilenmemiz yeterli. Denklemin sonunu getirmek için daha fazla detaya ihtiyaç duyabilirsiniz. Bu noktada, denklemler konusunda daha fazla pratik yapmak isterseniz, Superprof'taki uzman matematik öğretmenlerinden online dersler alarak kendinizi geliştirebilirsiniz!

Polinom Nedir?
Polinom, bir veya birden fazla değişkene sahip olabilen bir matematiksel ifadedir. Bir polinom, katsayılar ve değişkenlerin kuvvetlerinin toplamı şeklinde yazılır. En temel haliyle; n bir doğal sayı, a0, a1, a2, a3….an gerçek sayılar olmak üzere bir değişkenli polinom şu şekilde ifade edilir:
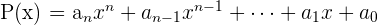
Bu ifadeyi şu şekilde örneklendirebiliriz:
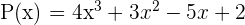
Bu polinomda x bilinmeyeninin en yüksek kuvveti 3 olduğu için, polinomun derecesi 3’tür.
Polinomlar, sıklıkla cebirsel işlemlerde ve denklemlerde karşımıza çıkar. Matematikte polinomların kullanım alanları oldukça geniştir; analitik geometri, türev ve integral hesaplamaları gibi birçok farklı alanda karşımıza çıkar.
Polinomların Türleri
Polinomlar, derecelerine ve terim sayılarına göre sınıflandırılabilir. En yaygın polinom türleri şunlardır:
- Sabit Polinom: Değişkenin olmadığı ya da tüm terimlerin sabit olduğu polinomlardır. Örneğin, P(x)=7 sabit bir polinomdur.
- Doğrusal Polinom (Birinci Dereceden Polinom): Değişkenin en yüksek kuvveti bir olan polinomlardır. Örneğin, P(x)=2x+3 doğrusal bir polinomdur.
- İkinci Dereceden Polinom (Kare Polinom): Değişkenin en yüksek kuvveti iki olan polinomlardır. Kare polinomlar genellikle şu şekilde yazılır: P(x)=ax^2+bx+c. Bu tür polinomlar, ikinci dereceden denklemlerde sıklıkla kullanılır.
- Üçüncü Dereceden Polinom (Kübik Polinom): Değişkenin en yüksek kuvveti üç olan polinomlardır. Örneğin, P(x)=x^3−2x^2+x−5 üçüncü dereceden bir polinomdur.
Polinomlar da denklemlerin başka bir türüdür. TYT ve AYT sınavlarına hazırlanırken karşınıza sık sık çıkacaktır. Polinom çıkmış sorular çözerek bu konuda bol bol pratik kazanabilirsiniz. Şimdi az önce bahsettiğimiz bölmeli denklemlerde yaptığımız işleme devam ederek polinom denklemleri de açıklığa kavuşturalım.
Polinomlarda Toplama ve Çarpma
Polinomlarla işlem yapmak, birçok matematiksel problemi çözerken gereklidir. İki polinomun toplanması veya çarpılması, genellikle terimlerin bir araya getirilmesi ya da çarpanlarına ayrılmasıyla yapılır.
Toplama: İki polinom toplandığında, aynı derecedeki terimlerin katsayıları toplanır.
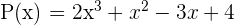
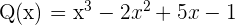
Polinomların toplamı:
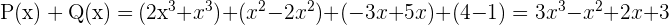
Çarpma: Polinomların çarpılması ise, her terimin birbiriyle çarpılması ve sonrasında terimlerin birleştirilmesiyle yapılır. Örneğin:
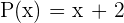
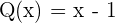
Polinomların çarpımı:
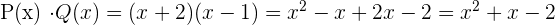
Bu tür işlemler, polinom denklemlerini çözerken ve matematiksel fonksiyonları analiz ederken sıklıkla kullanılır.
Denklemler ve Polinomların İlişkisi
Denklemler, bilinmeyen bir veya birden fazla değeri bulmak için kullanılan matematiksel ifadelerden oluşur. Denklem, bir eşitlik ile iki tarafın birbirine eşit olduğunu belirtir. Polinomlar ise, bu denklemlerin bir parçası olabilir. Örneğin, ikinci dereceden bir polinom denklem şu şekilde yazılabilir:

Bu tür bir denklemi çözmek için kullanılan yöntemlerden biri kök formülü veya tam kareye tamamlama yöntemidir. Ayrıca, faktörlere ayırma yöntemi de polinom denklemlerinin çözümünde sıklıkla kullanılır.
Bu denklemi faktörlere ayırarak çözeriz:
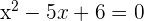
Bu durumda, denklemin kökleri
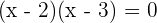
Polinom Denklemlerinin Çözüm Yöntemleri
Polinom denklemleri çözmek için birçok farklı yöntem vardır. İşte en yaygın kullanılan çözüm teknikleri:
- Faktörlere Ayırma: Polinomları çarpanlarına ayırarak, kökleri bulmak mümkündür. Bu yöntem, genellikle ikinci dereceden denklemler için uygundur.
- Kök Formülü: İkinci dereceden denklemleri çözerken kullanılan bir formüldür. Denklem şu şekilde yazılırsa:

Bu denklemin kökleri, şu formül ile bulunabilir
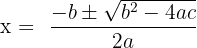
- Tam Kareye Tamamlama: Bu yöntem, denklemdeki terimleri düzenleyerek, bir tam kare ifade elde etme yoluyla denklemin çözülmesini sağlar.
- Polinom Bölmesi: Daha yüksek dereceli polinomların çözümlenmesi için kullanılan bir yöntemdir. Bu yöntemde, polinom bir başka polinoma bölünerek sadeleştirme yapılır ve kökler bulunur.

Sonuç
Polinomlar ve denklemler, matematiğin temel yapı taşlarından olup, cebirsel ifadeleri anlamak ve çözümlemek için kullanılır. Polinomlar, özellikle değişkenler ve katsayılar arasındaki ilişkileri modellemek için son derece kullanışlıdır. Denklemler ise, bu modellerin çözümünde önemli bir rol oynar. Polinomların doğru anlaşılması ve denklemlerin çözümlenmesi, matematikte ileri düzey problemlerin çözülmesine olanak tanır.
Matematikte polinomların ve denklemlerin uygulamaları, sadece teorik değil, pratik olarak da birçok alanda karşımıza çıkar. Özellikle mühendislik, fizik ve ekonomi gibi disiplinlerde, polinomlar ve denklemler, problem çözme sürecinde kritik bir yer tutar.
Polinom Denklemlerin Grafikleri
İster üçgen, ister dörtgen, ister çokgen! Herhangi bir şekli doğru denklemlerle cebirsel ifadeleri kullanarak bir grafik üstünde çizebileceğinizi biliyor muydunuz?
Denklemleri çözerken hangi adımları izlediğimizden bahsettiğimize göre polinom denklemlerin grafiğini nasıl çizebileceğinizi kısaca anlatalım.
Üssü iki veya daha fazla olan en az bir değişkeni olan denklemlere polinom denklemler denir.
Bu aşağıdaki denklem türlerini de içerir:
- Asimptotik denklemler
- Trigonometrik fonksiyonların denklemleri
- Logaritmik denklemler
Peki, bu tarz bir denklemin grafiğini nasıl çizebiliriz? Matematik özel ders ile detaylı öğrenebilecek olsanız da, bu adımda bir eğrinin ekstremum noktalarını (minimum ve maksimum değerlerini) bulmalı ve ardından eğriyi çizmeliyiz.

Bunun için bir "x" değerlerini denklemde yerine koyup "y" değerlerini bulabiliriz. Daha sonra kabaca eğrinin şeklini belirleriz. Böylece minimum ve maksimum değerlere ulaşabiliriz.
Orijinal denkleminize f(x) diyeceğiz ve türev fonksiyonuna f'(x) diyeceğiz. İzlememiz gereken adımlar şöyle:
- F(x) değerinin türevini alın.
- Eğrinin minimum ve maksimum değerlerini bulmak için f'(x) i çarpanlarına ayırın.
- Eğri üzerindeki noktaları bulmak için değerleri f(x) ile değiştirin.
- Bu noktaları bir grafikte işaretleyin.
- Minimum ve maksimum noktalara ulaştığınızdan emin olduktan sonra eğrinizi çizin.
Her zaman olduğu gibi burada da kilit nokta ayrıntılardır. Noktaları grafikte doğru şekilde işaretlediğinizden ve eğrinizin minimum ve maksimum noktalardan geçtiğinden emin olun.
Bu polinomlar konu anlatımı, grafik çizme, türev alma vs. hâlâ kafanızı karıştırıyorsa özel bir Ankara matematik öğretmeni yardımına danışabilirsiniz. Hangi kaynakla daha iyi hazırlanabileceğinizi öğrenebilirsiniz. Birlikte denklemler ve polinomlar çıkmış sorular çözebilir, hızlıca ilerleme kaydedebilirsiniz.
Yapay zekâ ile özetle