Bu yazımızda, 10. sınıf fizik müfredatında yer alan ve temel konular arasında bulunan Basınç ve Kaldırma Kuvvetini detaylı bir şekilde inceleyeceğiz. Bu konu, özellikle TYT sınavında sıkça karşımıza çıkan sorular arasında yer almakta. Bu nedenle, TYT fizik basınç bölümüne hazırlık sürecinde Basınç ve Kaldırma Kuvveti konusunu derinlemesine öğrenmeniz ve bol miktarda soru çözerek pratiğinizi artırmanız oldukça önemlidir. TYT Fizik basınç ve kaldırma kuvveti öğrenme sürecinizi daha etkili hale getirmek için bir fizik öğretmeninden destek almayı da düşünebilirsiniz.

Basınç Nedir?
Bir çok fizik probleminde önemli bir değişken olarak ortaya çıkan basınç, bir yüzeye uygulanan dik kuvvetin, yüzeyin birim alanına oranı olarak ifade edilir. Basınç, P simgesiyle gösterilir, türetilmiş ve skaler bir büyüklüktür, yani basıncın yönü yoktur. Aşağıdaki gibi formülleştirebiliriz.
P=F/A

Katılarda Basınç
Katı cisimler bulundukları yüzeye ağırlıklarından dolayı basınç uygular. Basıncın büyüklüğü, cismin ağırlığından cismin yüzey ile temas eden yüzey alanından ve yüzeyin eğiminden etkilenir. Katılarda basınç kuvveti ekstra bir durum yok ise katı cismin ağırlığına eşittir.
Ekstra olan durum katı cismin üzerine herhangi bir kuvvet uygulanıp uygulanmadığıdır. Katılar üzerine uygulanan kuvveti aynı doğrultuda aynen iletirler. Bundan dolayı katı cismin zemine uyguladığı kuvvet değişecektir.
Basınç P, kuvvet F ve yüzey alanı da S ile gösterilirse,
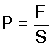
Bu bağıntıya göre, kuvvet sabit ise, basınç yüzey alanı ile ters orantılıdır.
Yüzey alanı sabit ise basınç, kuvvet ile doğru orantılıdır.
- Sivri uçlu çivinin ucundaki basınç büyük olduğu için küt uçlu çiviye göre daha kolay çakılır.
- Bıçak köreldiği zaman bilenerek yüzey alanı küçültülür ve basıncın artması sağlanır. Bu nedenle aynı kuvvetle daha kolay kesme işlemi sağlanmış olur.
- Topuklu ayakkabılarının ince topukları, kişinin vücut ağırlığını çok küçük bir yüzey alanına ilettiği için çok daha büyük bir basınç oluşturur. Bu durum, ayakkabının sert zeminlerde hızlı bir şekilde aşınmasına veya batmasına yol açabilir.
Daha önce de bahsettiğimiz gibi, katılar kendilerine uygulanan kuvveti aynı yönde ve aynı büyüklükte iletirler. Fakat basıncı iletmezler.
Örneğin bir çivinin baş kısmına kuvvet uygulandığında bu kuvvet sivri uca da aynen iletilir. Dolayısıyla sivri ucun yüzey alanı küçük olduğundan basınç daha büyük olur.
TYT'nin önemli konularından biri olan Optik konusunu detaylarıyla anlattığımız yazımıza göz atın.
Gaz Basıncı
Gazların belirli bir hacmi ve şekli yoktur. Gazlar içerisine konulduğu kabı homojen bir şekilde tamamen kaplar. Bu nedenle gazın hacmi ve şekli, kabın hacmi ve şekliyle aynı olur. Gaz molekülleri arasındaki boşluk fazla olduğu için gazlar sıkıştırılabilir.
Gazların basıncı P.V=n.R.T formülü ile bulunur.
- Kapalı kaptaki gazların basınçlarını ölçmek için kullanılan aletlere manometre denir.
Kapalı kaptaki gazların basıncı genel olarak üç niceliğe bağlıdır.
- Sıcaklık ve hacim sabit ise gaz basıncı molekül sayısı ile doğru orantılıdır. (P ~ n)
- Sıcaklık ve molekül sayısı sabit ise, kabın yani gazın hacmi ile ters orantılıdır. Hacim arttıkça basınç azalır, hacim azaldıkça basınç artar.
- Hacim ve molekül sayısı sabit ise, gazın basıncı mutlak sıcaklıkla doğru orantılıdır. Sıcaklık arttıkça gaz moleküllerinin hızı artar ve kabın iç yüzeyinde birim alana çarpma sayısı artar. Bu da basıncın artmasına neden olur.
Açık Hava (Atmosfer) Basıncı Dünya'nın çevresinde bulunan kilometrelerce kalınlıktaki gaz kütlesinin ağırlığından ve gaz moleküllerinin sahip olduğu kinetik enerjilerinden dolayı oluşan basınca açık hava basıncı denir. Açık hava basıncı Po sembolüyle gösterilir. Yer yüzeyinden yukarı çıkıldıkça atmosferdeki gaz molekülleri seyrekleştiği için açık hava basıncı azalır.
Açık hava basıncını ölçen alete barometre denir.
Toriçelli Deneyi Evangelista Torricelli 1644 yılında çok önemli bir deney yaptı. Deniz seviyesinde 0°C sıcaklıkta, yaklaşık 1 metre uzunluğundaki bir ucu açık diğeri kapalı bir cam tüpün içini tamamen cıvayla doldurdu. Sonra cam tüpün açık olan ucunu parmağıyla kapatarak cıva dolu bir kabın içine yerleştirdi. Ardından parmağını açık uçtan çekti. Cam tüpün içindeki cıvanın bir miktarı kaba boşaldı, ama yüksekliği 760 mm olacak kadar bir kısmı tüpün içinde kaldı.
Cıvanın neden tamamı boşalmadı?
Çünkü kaptaki cıvaya uygulanan açık hava basıncı cam tüpün içindeki cıvayı yukarı doğru itti. Tüpün içindeki cıvanın sıvı basıncı açık hava basıncına eşit hale geldi. Bu dengelenme ilkesini kullanarak barometreler yapıp açık hava basıncını ölçebiliyoruz.
Patmosfer = Pcıva Pcıva = hdcıvag Pcıva = 0,76 m x 13534 kg/m3 x 9,81 m/s2 Pcıva = 101,3 kPa Patmosfer = 101,3 kPa = 1 atm
Kaldırma Kuvveti
Fizik basınç konu anlatımı bittiyse sırada kaldırma kuvveti var! Sıvıya batırılan bir tahta parçası yukarı çıkmak ister. Tahta parçasının tamamını batacak şekilde sıvı içinde tutabilmek için üstten bir kuvvet uygulamak gerekir. Sıvıya bırakılan cisimlere sıvı tarafından aşağıdan yukarıya doğru bir kuvvet uygulanır. Bu kuvvete sıvının kaldırma kuvveti denir. Kaldırma kuvveti cisim sıvıya nasıl bırakılırsa bırakılsın batan kısmının tam ortasına aşağıdan yukarıya doğru uygulanan kuvvettir. Sıvıların kaldırma kuvveti şunlara bağlıdır;
- cismin sıvıya batan hacmine (V batan)
- sıvının yoğunluğuna (d sıvı)
- yer çekim ivmesine (g)
Fkaldırma = Vbatan dsıvı g
Bir cismi sıvıya bıraktığımızda üç değişik şekilde dengede kalabilir. Suyun yüzeyinde kalan cisimlere yüzen cisim (cismin özkütlesi sıvının özkütlesinden küçüktür), suyun içinde dengede kalan cisimlere askıda kalan cisim, dibe çöken cisimlere ise batan cisim denir.

Şekil l ve Şekil II deki gibi yüzen ve askıdaki cisimlere uygulanan kaldırma kuvveti cismin ağırlığına eşittir. Şekil III teki gibi batan cisimlere uygulanan kaldırma kuvveti ise cismin ağırlığından küçüktür.
TYT’de soru çıkma ihtimali yüksek olan dalgalar konusunu da çalışmayı unutmayın.

Arşimet Yasası
Matematikçi, gökbilimci, mühendis ve mucit olan Arşimet (MÖ 287 - MÖ 212), Eski Yunan tarihinin en parlak zekalarından biri olarak bilinir. Kaldırma kuvveti, yoğunluk, makaralar ve kaldıraçlar üzerindeki çalışmalarıyla tanınan Arşimet, aynı zamanda geometriye yaptığı önemli katkılarla da öne çıkmıştır.
Efsaneye göre, Arşimet güneş ışınlarını düşman gemilerine odaklayarak onları tutuşturabilecek bir ayna düzeneği geliştirmiştir. Bu hikâye, Arşimet’in dahiyane zekasının yalnızca bir göstergesidir. Eğer bu konularla ilgileniyorsanız, İzmir’in fizik öğretmenleri, Ege Denizi’nin kıyısında belki de bu tür olayları en etkili şekilde açıklayabilecek kişiler olabilir!
Arşimet’in dehasını gösteren en ünlü hikâyelerden biri, MÖ 3. yüzyılda Yunan kültürünün önemli bir merkezi olan Sicilya'nın Siracusa kentinde geçer. Şehrin kralı II. Hieron, krallık kuyumcusunun kendisi için yaptığı tacın saf altından olmadığı, içine gümüş karıştırıldığı şüphesine kapılır. Kral, kandırılıp kandırılmadığını öğrenmek için Arşimet’e başvurur.
Bu zor bir görevdi; çünkü Arşimet tacı eritmeden ya da zarar vermeden altının saflığını tespit etmek zorundaydı. Kimyasal analiz yöntemlerinin henüz bilinmediği bir dönemde, bu sorunu çözmek için yenilikçi bir yol bulması gerekiyordu. Arşimet’in bu süreçte gerçekleştirdiği deneyler, günümüzde yoğunluk ve kaldırma kuvvetine ilişkin bilgilerimizin temelini oluşturmuştur.
Hareket ve Kuvvet ders anlatımını okumayı unutmayın.
Arşimet bir gün, küvetin içine oturmuş bu sorunu düşünürken, sıvıya batırılan bir cismin, kendi hacmine tam olarak eşit miktarda suyu taşırdığını anlıyor. Banyo fıçısından yere taşan suyun hacmi ölçülürse fıçının içindeki nesnenin hacmi elde edilir. İşte bu noktada Arşimet, “Evreka! Evreka!” diye bağırarak evine doğru koşmaya başlıyor; varınca da önce som altın parçasını, sonra som altından yapıldığı söylenen tacı bir leğene koyuyor.
Taç, som altın parçasına kıyasla suyun daha fazla yükselmesine neden olunca, hacminin daha büyük olduğu (ve bu nedenle yoğunluğunun daha düşük olduğu, yani som altından olmadığı) açığa çıkıyor. Böylece kuyumcunun da suçlu olduğu anlaşılıyor.

Bu ilke, gemilerin niçin yüzdüğüne ek olarak, balonların nasıl yükseldiğini de açıklamakta ve neyin batıp neyin batmayacağını, neyin yüzüp neyin yüzmeyeceğini, neyin uçup neyin uçmayacağını belirlerken, biçim ve konumdan başka, ağırlık ve hacmin de göz önünde bulundurulması gerektiğini söylemektedir.
Kaldırma kuvveti, nesnenin ağırlığına karşılık verir ve eşit kuvvette yukarı iter. Ancak nesne, yer değiştirdiği suyun hacminden daha ağırsa (yani sudan yoğunsa) batar. Arşimet bu mantığı kullanarak kralın tacının saf olmadığını kanıtlamıştır.
Bu ilke hala mücevher gibi pahalı nesnelerin saflığını ölçmede kullanılıyor.
Ankara fizik öğretmeni ve Türkiye'nin 81 ilindeki fizik öğretmenleri ile kaldırma kuvveti ve basınç TYT çalışabilirsiniz.
Quiz
Quiz :Yapay zekâ ile özetle