Türev, reel sayılardan reel sayılara giden tek değişkenli fonksiyonlar için tanımlanmış, herhangi bir teğetin herhangi bir eğriye x ekseniyle yaptığı pozitif yönlü açının tanjant değeridir.
Daha basit bir deyişle bir şeyin bir diğer şeye göre değişim miktardır. Yani değişimi ölçmek için kullanılır diyebiliriz. Bir şeyin zaman geçtikçe ne kadar değiştiğini hesaplamak veya ifade etmek için kullanabiliriz.
İntegral ise türevin tersidir. Eğrilerin altındaki ve aralarındaki boşlukları hesaplamak için kullanılır.
Bu makalemizde matematiğin bu iki konusundan bahsedeceğiz. Günlük hayatımızda nerelerde kullanıldığını görünce daha iyi anlayabileceksiniz.
Ama aslında matematik her yerde, yaptığımız her şeyde var. Çiftliğimizdeki tavukları saymaktan, elimizdeki parayı hesaplamaktan bir barajın kapasitesini veya bir binada kullanılan malzeme sayısını bilmemizi sağlayan türev gibi matematikteki daha gelişmiş hesaplamalara kadar.
Doğru, az önce bahsettiğimiz bir binada kullanılan malzeme sayısı veya üretilen bir tankın alabileceği toplam su miktarı, hatta kâr ve zarar gibi hemen hemen her şeyin maksimum ve minimum değerini hesaplayabilir ve bulabilirsiniz.
Alttaki yüke zarar vermeden bir yükü ne kadar yükseğe çıkarmanız gerektiğini bulmak için türevi kullanabilirsiniz.
Eğitim hayatınızda ve kariyerinizde mühendisliği düşünüyorsanız türevle aranızı iyi tutmalısınız. Türevi sayılarla ilgili her türlü sorunu çözmek için kullanacaksınız. Ancak herhangi bir teknik kariyere düşünmüyorsanız daha az türev ve integral görebilirsiniz.
Tabii finans sektöründe çalışacaksanız da bu konuya ihtiyacınız olacak. Bir şeyin maliyetini tahmin etmek, değerlendirmek ve bir girişimin kârlılığını hesaplamak için türevden büyük ölçüde yararlanacaksınız.
Yani anlayacağınız türev, ekonomimiz ve altyapımız için hayati önem taşıyan bir konudur. Birçok matematik problemini çözmemize yardımcı olur ve aynı zamanda çeşitli endüstrilerde başarabileceklerimizin maksimumunu doğru bir şekilde tahmin etmemize yardımcı olur, böylece zamandan ve emekten tasarruf etmemizi sağlar.
Antik çağlardan beri güvenli bir deniz yolculuğu yapmak için yıldızların ve ayın konumunu çözmek için kullanılmıştır. Türev bizim için o kadar çok faydalıdır ki kullanım alanları saymakla bitmez
İş ararken bu gibi konularda iyi bir bilgi birikimine sahip olmak, sizi diğer adayların önüne taşıyacaktır.
Bir Fonksiyonun Bir Noktadaki Türevi
Belirli bir fonksiyonun anlık değişim oranı hesabın temelidir. Temel olarak herhangi bir noktada bir fonksiyonun değişim oranını ölçer. Belirli bir zaman aralığında hareket eden bir nesnenin hızını ölçen anlık hız kavramına benzer. Bir fonksiyonun hareket halindeki bir nesne olduğunu varsayarsak, o zaman anlık değişim oranı, hareket hâlindeki nesnenin hızı anlamına gelir.
Anlık değişim oranını gerçek hayatımızda da kullanırız. Örneğin, hızını saatte 1 kilometre artırdığımızda arabanın günlük kullandığı litre benzin miktarını ölçmek istediğimizde anlık değişim oranını kullanırız. Anlık bir değişim oranını grafikte de gösterebiliriz.
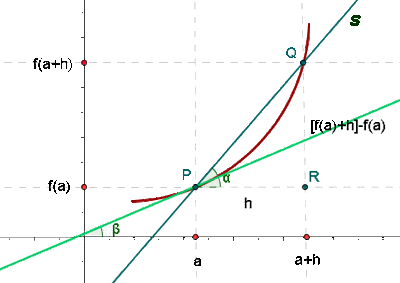
Limitle Bir Fonksiyonun Türevini Hesaplama
fonksiyonunun 
'daki türevi, 
değişkeninin sıfıra yöneldiği bu noktada varsa limitin değeridir.
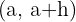aralığındaki anlık değişim oranı aşağıdaki formülle gösterilen 
fonksiyonunu inceleyelim:
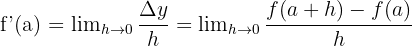
Yukarıdaki formülü kullanarak fonksiyonların türevlerini nasıl hesaplayacağımıza bir bakalım.
Örnek 1
ise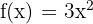 
fonksiyonunun türevini bulun.
Çözüm 1
Türev tanımını kullanarak çözüm yapalım:
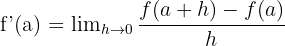
Bu durumda 
olduğu için:
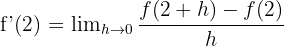
Fonksiyon 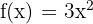olduğundan:
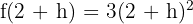
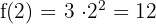
Bu değerleri türev formülüne yerleştirelim:
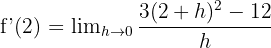
Parantez içindeki terimi açalım:
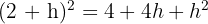
Bu ifadeyi yerine koyalım:
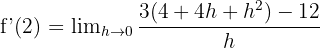
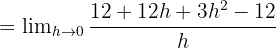
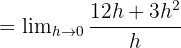
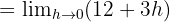
Şimdi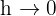 
için limiti alalım:
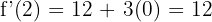
Örnek 2
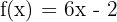fonksiyonunun türevini limit formülüyle bulalım.
Çözüm 2
Türevi hesaplamak için aşağıdaki limit formülünü kullanacağız:
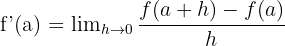
Bu örnekte 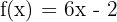olduğu için:
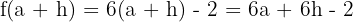
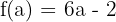
Bu değerleri türevin limit formülüne koyalım:
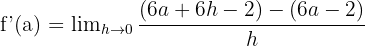
Paydaki parantezi açarak ifadeyi çözelim:
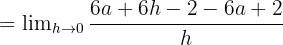
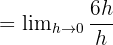
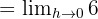
Limit değeri:
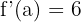
Örnek 3
Aşağıdaki fonksiyonun türevini limit formülüyle hesaplayın:
Çözüm 3
Türevi hesaplamak için limit formülünü kullanacağız:
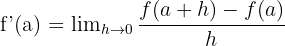
Bu örnekte olduğu için:
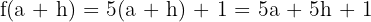
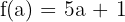
Bu değerleri türevin limit formülüne koyalım:
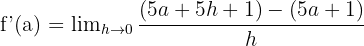
Paydaki parantezi açarak ifadeyi çözelim:
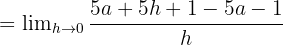
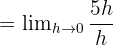
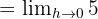
Limit değeri:
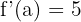
İntegral Nedir?
Matematikte, integraller bize bir şekilde yardımcı olan birkaç niceliği bulmak için kullanılır. Bu nitelikler hacimleri, alanı ve yer değiştirmeyi vb. içerir. Bir fonksiyonun integralini hesapladığımızı söylediğimizde, genellikle o fonksiyonun belirli integralini kastederiz. Ters türevler için belirsiz integraller kullanırız. İntegral sembolü ise şudur: ∫
Analizde, cebir ve geometri problemleriyle uğraşırken limit kavramını kullanırız.
Analizde iki temel kavram vardır: Türev ve integral. İntegral, ters bir farklılaşma sürecidir. Ayrık verilerin toplamını ifade eder. Bu, integral bulma sürecinin, bütünü hesaplamak için tek tek parçaları toplamakla ilgili olduğu anlamına gelir. İntegral bulma yöntemi, toplamı geniş bir ölçekte hesaplamak için kullanılır. Hesap makinelerini kullanarak küçük toplama problemlerine kolayca cevap bulabiliriz, ancak daha büyük problemler için integrali kullanırız. Bu problemlerde bazen sınırlar sonsuza kadar ulaşır. İntegral bulmanın amacı hacim, alan, yer değiştirme gibi küçük verilerden dolayı tekil olarak bulamadığımız fonksiyonları bulmaktır.
Matematikte İntegral Türleri
Bir önceki bölümde integral kavramından ayrıntılı olarak bahsettik. Şimdi matematikte iki tür integralin ne olduğunu göreceğiz. İki tür integral vardır:
- Belirli integral
- Belirsiz integral
Belirli İntegral
Üst ve alt sınırları olan bir integral, belirli integral olarak bilinir.
Belirli bir integral şu şekilde gösterilir:
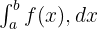
Belirsiz İntegral
Üst ve alt limit içermeyen integral, belirsiz integral olarak bilinir.
Belirsiz bir integral şu şekilde gösterilir:
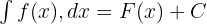
Burada:
bir sabittir.
, fonksiyonunun ters türevidir.
İntegral Kuralları
Soruları çözmenizi kolaylaştırması için şu kurallara hâkim olmanız gerekiyor:
Sabit Kuralı:
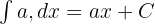
Sabit ile Çarpma:
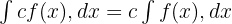
Kuvvet Kuralı:
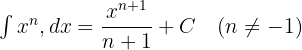
Toplam/ Fark Kuralı:
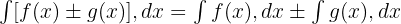
İntegral Soruları Nasıl Çözülür?
Şimdi birkaç örnekle bu bilgileri pekiştirelim.
Örnek 1
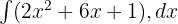kaçtır?
Çözüm 1:
İntegrali Parçalara Ayırma: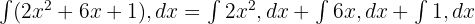
Sabitleri Dışarı Alma: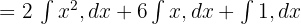
Kuvvet Kuralını Uygulama:
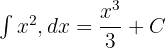
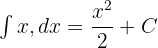
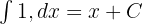
Sabitlerle Çarpma: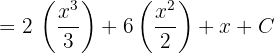
Sadeleştirme: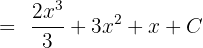
Örnek 2
Aşağıdaki üstel fonksiyonun integralini hesaplayın:
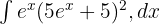
Çözüm:
İfadeyi Genişletme: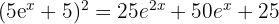
Bu durumda integral: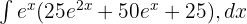
İntegrali Parçalara Ayırma: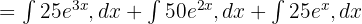
Her Terimin İntegralini Hesaplama:
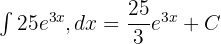
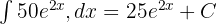
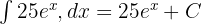
Sonucu Birleştirme: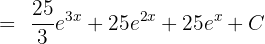
Örnek 3
Aşağıdaki fonksiyonun belirli integralini bulun:
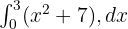
Çözüm:
Belirsiz İntegrali Bulma (Ters Türev):
fonksiyonunun ters türevi: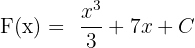
Belirli İntegral Formülü: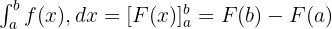
Ters Türevde Değerleri Yerine Koyma:
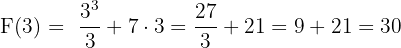
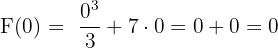
Sonucu Hesaplama: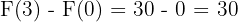
Bir Superprof Öğretmeniyle Türev ve İntegral Dersleri
İnternet, iletişim kurmanın inanılmaz bir yolu olduğu gibi çok yönlü bir öğrenme aracıdır.
Nerede yaşıyor olursanız olun, online ders her yere kapıları açar. Öğretmeniniz farklı bir ülkede bile yaşıyor olabilir ama internet sayesinde onunla iletişim kurabilirsiniz. Türev ve integrale kadar herhangi bir konu için özel derse ihtiyacınız varsa size yardımcı olabilecek birini hemen bulabilirsiniz.
Superprof gibi platformlarda özel dersler veren profesyonellerle kafanızı karıştırmadan ilerleme kaydedebilirsiniz.
Eğer öğretmen yanınızda olunca daha iyi odaklanıyorsanız yaşadığınız yerdeki öğretmenleri de Superprof'ta bulabilirsiniz.
Özel derslerin birçok avantajı var:
- Yaşadığınız yerde bir öğretmen bulabilirsiniz: Web sitesi otomatik olarak size en yakın öğretmenleri gösterir. Böylece çok da uzağa gitmeden matematik dersleri almaya başlayabilirsiniz.
- İhtiyacınız olan becerilere sahip birini bulabilirsiniz: Öğretmenlerin sayfalarında deneyimlerinin kısa bir açıklamasını görebilirsiniz. Saatlik ders ücretini, aldığı eğitimleri ve ders verdiği öğrencilerin yorumlarını da inceleyebilirsiniz.
- Bütçenize uygun dersler bulabilirsiniz: Herkesin özel derse ayırabileceği bütçe farklıdır. Kendi bütçenize göre özel matematik derslerini görüntüleyebilirsiniz. Ankara matematik özel ders ve diğer matematik özel ders seçenekleriniz için Superprof'un kolay ve anlaşılabilir arayüzünden araştırma yapabilirsiniz.
- Bazı öğretmenler ücretsiz deneme dersleri sunar: Bazı öğretmenler, sizin için doğru öğretmeni seçmenize yardımcı olmak için ilk dersi ücretsiz sunar. Seçtiğiniz öğretmenin doğru olmadığını düşünüyorsanız hemen başka bir öğretmen deneyebilirsiniz.
Ders çalışma programınızı öğretmeniniz sizin ihtiyaçlarınıza göre hazırlayacağından sizin yapmanız gereken tek şey ders çalışmaya odaklanmak olacak. Böylece türev ve integral problemlerini çözmek için daha çok vaktiniz olacak!
Bu yazıyı beğendiniz mi? Puanlayın!
Loading...
