Bir fonksiyonun türevi, fonksiyonun çıktısının girdi değerine göre değişim oranıdır. y = f(x) verildiğinde, f'(x) (veya df(x)/dx) ile gösterilen f(x)'in türevi aşağıdaki limitle tanımlanır:
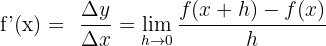
Türevin tanımı, bir doğrunun eğimi formülünden türetilir. Bir doğrunun eğiminin, y'deki değişimin x'teki değişime oranı olarak hesaplanan doğrunun değişim oranı olduğunu hatırlayın. Geometrik olarak türev, belli bir noktada eğriye teğet doğrunun eğimidir. Bazen anlık değişim oranı olarak adlandırılır. Tipik olarak, bir doğrunun eğimini, doğru üzerindeki iki noktayı kullanarak hesaplarız. Bir eğrinin eğimi noktadan noktaya değiştiği için bu bir eğri için mümkün değildir. Aşağıdaki şekle bir bakalım.
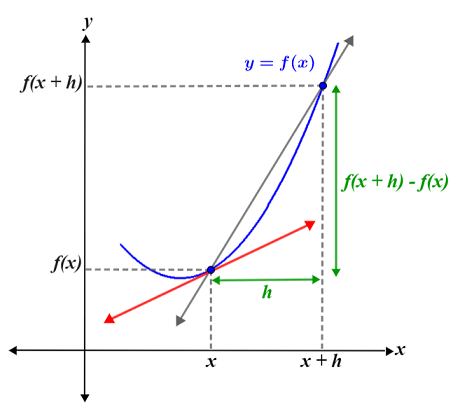
Şekilde iki noktalı bir eğri (mavi) gösterilmektedir: (x, f(x)) ve (x + h, f(x + h))). Gri çizgi, bu iki nokta arasındaki eğimi temsil eder ve şu şekilde hesaplanır:
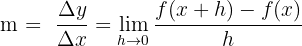
Az önce bahsettiğimiz türevin tanımına benziyor, değil mi? Ancak bu formül bize eğrinin eğiminin ortalaması olan iki nokta arasındaki eğimi verir. x'teki türev şekilde kırmızı çizgi ile gösterilmiştir. Bu doğrunun eğimini hesaplamak için, eğim formülünü tek bir nokta için kullanılabilecek şekilde değiştirmemiz gerekir. Bunu, h ile gösterilen x'teki (Δx) değişim 0'a yaklaşırken eğim formülünün sınırını hesaplayarak yaparız. Bunu yaparak, çok küçük bir farkla ayrılmış iki nokta arasındaki eğimi buluruz. Tek bir noktadaki eğim, bizi yukarıda belirtilen türevin tanımına götürür.

Türev Alma Kuralları
a, b birer reel sayı olmak üzere,
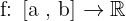 fonksiyonunu ele alalım.
fonksiyonunu ele alalım.
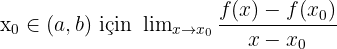
Bu limit bir reel sayı ise bu limit değerine "f fonksiyonunun  'daki türevi" denir.
'daki türevi" denir.
f'( ), Df(
), Df( ) ya da
) ya da 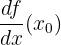 ile gösterilir.
ile gösterilir.
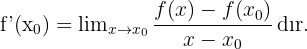
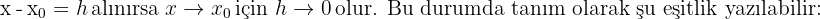
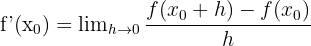

Başka bir duruma bakalım.
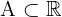 ve
ve 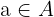 olsun.
olsun. 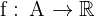 fonksiyonunda
fonksiyonunda
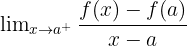
limiti varsa bu limite f fonksiyonunun  'daki sağdan türevi denir.
'daki sağdan türevi denir.
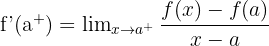 şeklinde gösterilir.
şeklinde gösterilir.
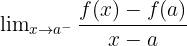
Ayrıca 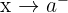 limiti varsa bu limite f fonksiyonunun
limiti varsa bu limite f fonksiyonunun  'daki soldan türevi denir.
'daki soldan türevi denir.
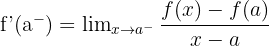 şeklinde gösterilir.
şeklinde gösterilir.
f fonksiyonunun, x = a'daki sağdan türevi soldan türevine eşit ise f'nin x = a'da türevi vardır ve bulunan bu limit değerleri, o noktadaki türeve eşittir. Böyle bir durum yoksa türevi yoktur.
- f ‘(a+) = f'(a–) ise f fonksiyonunun x = a'da türevi vardır.
- f fonksiyonunun x = a'da türevi varsa f fonksiyonu x = a'da süreklidir.
- f fonksiyonu, x = a'da sürekli olduğu hâlde, o noktada türeve sahip olmayabilir.
- f fonksiyonu x = a'da sürekli değilse türevli de değildir.
- Bir fonksiyonun, bir noktada türevinin olması için o noktada süreklilik gerekir. Tabii bu tek başına o noktada türevin olması için yeterli olmaz.
Şimdi gelelim genel türev alma kurallarına.
 ’nin Türevi
’nin Türevi
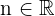 olmak üzere,
olmak üzere,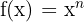 ise
ise 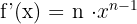 dir.
dir.
 Sabit Sayısının Türevi
Sabit Sayısının Türevi
 olmak üzere,
olmak üzere,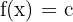 ise
ise 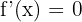 dir.
dir.
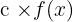 ’in Türevi
’in Türevi
 olmak üzere,
olmak üzere,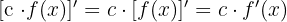 tür.
tür.
Toplamın Türevi
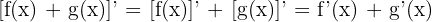
Farkın Türevi
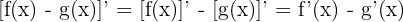
Çarpımın Türevi
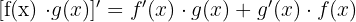
Bölümün Türevi
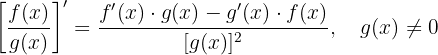
Mutlak Değer Fonksiyonunun Türevi
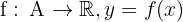
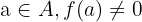 olmak üzere,
olmak üzere,
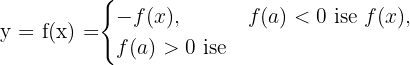
f(a) = 0 ise fonksiyonun bu noktada türevi olabilir ya da olmayabilir. Bunu araştırmak için fonksiyonun sağdan ve soldan türevlerine bakılır. Sağdan ve soldan türevler eşit ise fonksiyon bu noktada türevlidir. Değilse türevli değildir.
- Mutlak değer fonksiyonu tek katlı köklerde köşe (uç) oluşturur. Köşe (uç) noktalarda türev yoktur
- Çift katlı köklerde köşe (uç) oluşmaz. Bunun için, çift katlı köklerde türev vardır ve sıfırdır.
İşaret Fonksiyonunun Türevi
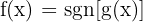 ise
ise
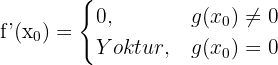
Tam Değer Fonksiyonunun Türevi
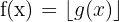 ise
ise
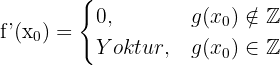
Bileşik Fonksiyonun Türevi
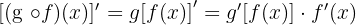
- f ‘(2) gösterimi [f(2)]’ gösterimi ile karıştırılmamalıdır.
- f ‘(2) ¹ [f(2)]’ dir. Çünkü f ‘(2) gösterimi, fonksiyonun türevinin, yani f ‘(x) in x = 2 için değeridir.
- [f(2)]’ gösterimi, fonksiyonun x = 2 için değerinin (Yani, bir reel sayının) türevidir. [f(2)]’ = 0'dır.
Kuralımız şöyle:
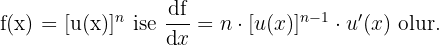
Köklü Fonksiyonun Türevi
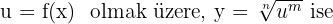
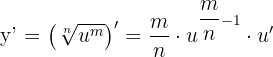
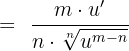
Yani kuralımız şöyle:
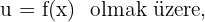
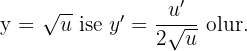
Logaritmik Fonksiyonun Türevi
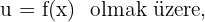
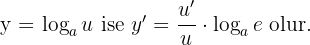
Burada kuralı şöyle verebiliriz:
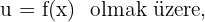
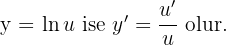
Üstel Fonksiyonun Türevi
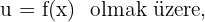
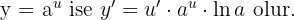
Kural:
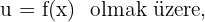
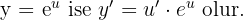
Parametrik Olarak Verilen Fonksiyonların Türevi
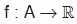
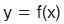
y = g(t)
x = h(t)
denklemleri ile de belirtilebilir. Burada t'ye "parametre" denir.
Bazen y = g(t) ve x = h(t) denklemlerinden t yok edilerek y = f(x) şeklinde bir denklem elde edilebilir. Ama bu her zaman mümkün olmayabilir.
Öyle bir durumda:
y = g(t), x = h(t) parametrik denklemleriyle verilen
y = f(x) fonksiyonunun türevi aşağıda verilen kural yardımıyla bulunur.
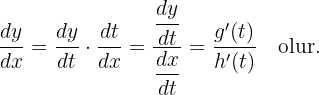
Kapalı Fonksiyonların Türevi
F(x, y) = 0 biçimindeki fonksiyonlara kapalı fonksiyon denir.
x'in değişken, x'in dışında kalanların sabit gibi düşünülmesiyle alınan türevi Fx ile; y'nin değişken, y'nin dışında kalanların sabit gibi düşünülmesiyle alınan türevi Fy ile gösterelim.
Buna göre, kapalı fonksiyonun türevinin kuralı şudur:
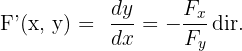
Trigonometrik Fonksiyonların Türevi
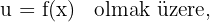
Ardışık Türevler
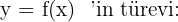
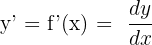 olmak üzere
olmak üzere
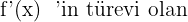
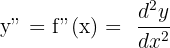 ifadesine
ifadesine
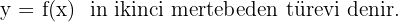
Benzer şekilde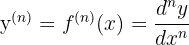
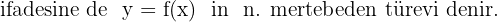
Kurallar şöyle:
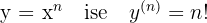
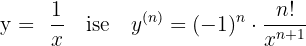
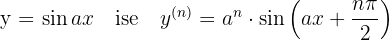
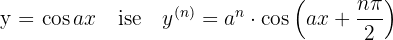
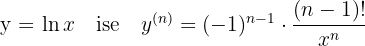
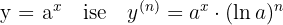
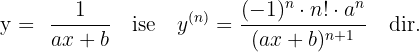
Ters Fonksiyonların Türevi
f: A -> B, birebir ve örten bir fonksiyon ise f(x) in tersi olan f–1(x) fonksiyonu bulunur. Sonra türev alınır. Bunun zor olduğu durumlarda ters fonksiyonun türevi şöyle alınır.
Bunun zor olduğu durumlarda ters fonksiyonun türevi şöyle alınır:
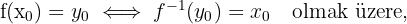
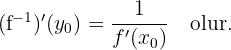
Ters trigonometrik fonksiyonların türevinin bulunmasında şu formüller kullanılabilir.
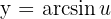 ise
ise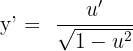
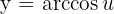 ise
ise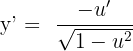
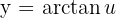 ise
ise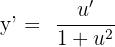
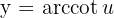 ise
ise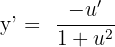
Türev Alma Örnekleri
 diyelim:
diyelim:
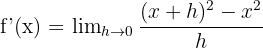
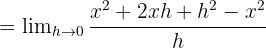
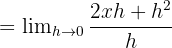
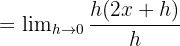
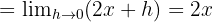
Böylece  türevi 2x'tir. Belirli bir noktadaki türevi bulmak için x değerini yerine koyarız. Örneğin, x = 1'deki türevi bilmek istiyorsak, şunu bulmak için türevi 1'e koyarız:
türevi 2x'tir. Belirli bir noktadaki türevi bulmak için x değerini yerine koyarız. Örneğin, x = 1'deki türevi bilmek istiyorsak, şunu bulmak için türevi 1'e koyarız:
f'(x) = f'(1) = 2(1) = 2
Başka bir örnekle devam edelim.
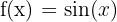 :
:
Bu sorunu çözmek için aşağıdaki trigonometrik kimlikleri ve limitleri kullanacağız:
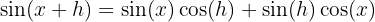
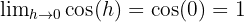
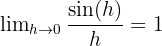

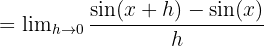
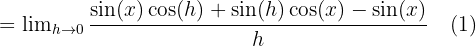
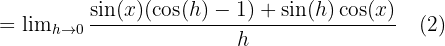
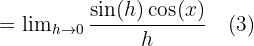
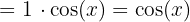
Böylece, 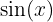 ’in türevi
’in türevi 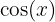 olur veya şöyle gösterebiliriz:
olur veya şöyle gösterebiliriz:
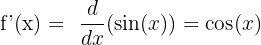

Örnek:
Aşağıdaki işlemlerin diferansiyelini hesaplayın
Çözüm:
Örnek
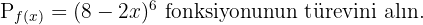
Çözüm
İlk olarak, 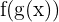 şeklinde yazıldığı için yukarıdaki fonksiyonu hemen bileşik fonksiyon olarak tanımlamalıyız. Bu örnekte:
şeklinde yazıldığı için yukarıdaki fonksiyonu hemen bileşik fonksiyon olarak tanımlamalıyız. Bu örnekte:
Adım 1: 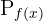 'in türevini bulalım.
'in türevini bulalım.
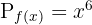 ise kuvvet kuralını kullanarak türevini bulabiliriz:
ise kuvvet kuralını kullanarak türevini bulabiliriz:
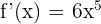
Adım 2: 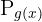 'in türevini bulalım.
'in türevini bulalım.
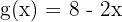 ise türevi:
ise türevi:
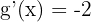
Adım 3: Zincir kuralını uygulayalım.
Zincir kuralına göre:
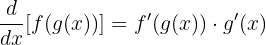
Bu durumda:
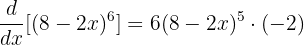
Adım 4: İfadeyi sadeleştirelim.
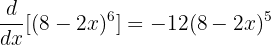
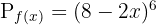 fonksiyonunun türevi:
fonksiyonunun türevi:
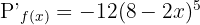

Örnek:
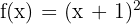 fonksiyonunun türevini bulun.
fonksiyonunun türevini bulun.
Çözüm:
Yukarıdaki fonksiyon,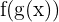 şeklinde yazıldığı için bileşik bir fonksiyondur.
şeklinde yazıldığı için bileşik bir fonksiyondur.
Burada:
Adım 1:  ve
ve  'in türevlerini bulalım.
'in türevlerini bulalım.
 ise türevi:
ise türevi:
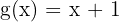 ise türevi:
ise türevi: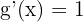
Adım 2: Zincir kuralını uygulayalım.
Zincir kuralına göre: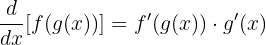
Bu durumda: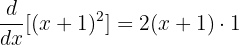
Adım 3: İfadeyi sadeleştirelim.
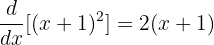
Sonuç:
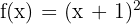 fonksiyonunun türevi:
fonksiyonunun türevi: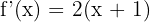
Bir Özel Ders Öğretmeniyle Türev Öğrenme
Özel dersler, çalışma ve öğrenme becerilerinizi geliştirmenize yardımcı olabilir. Bu da hayatınız boyunca başarıya ulaşmanızı sağlamaya yardımcı olur. Özel derslerin birçok avantajı vardır.
Bireysel ve benzersiz öğrenme deneyimini tadarsınız. Öğretmeniniz dersleri size ve ihtiyaçlarınıza göre uyarlayabilir. Ayrıca özel derslerde öğretmenin dikkati sizde olur. Bireysel öğrenme stilinizi tanır ve öğretim yöntemlerini buna göre uyarlayabilir.
Özel dersler almak, akademik performansı artırır. Özel derslerde öğretmeniniz sizi testlere ve sınavlara hazırlarken güçlü yanlarınızı ortaya çıkarır ve zayıf olduğunuz noktalarda size yardımcı olur. Hem tek başınıza nasıl ders çalışacağınızı daha iyi anlarsınız. Öğretmeninizden farklı çalışma teknikleri öğrenirsiniz. Kendisinden size bir çalışma programı hazırlamasını isteyebilirsiniz.
Alacağınız özel derslerle kendinize olan güveniniz de artar. Öğretmeniniz başarılı olmak için ihtiyaç duyduğunuz kaynakları ve becerileri sağlayarak öz güveninizi arttırabilir. Pozitif çalışma alanı yaratarak özel derslerde öğrenmeye daha iyi odaklanırsınız. Etrafınızda dikkat dağıtan kimse olmaz.
Özel matematik öğretmeni, öğrenme engellerinizin üstesinden gelmenize yardımcı olur. Öğrenmenin hangi alanında sorun yaşıyorsanız öğretmeniniz onu özellikle hedef alacaktır. Tam ihtiyacınız olan eğitimi alırsınız. Böylece vaktinizi en iyi şekilde değerlendirmiş olursunuz. Emin adımlar atarak hızla ilerlersiniz!
Superprof'taki özel ders öğretmenlerinden isterseniz sadece türev konusunda yardım alabilirsiniz. Sadece soru çözümleri yapabilirsiniz. Matematik özel ders ve matematik özel ders Ankara seçenekleriniz için Superprof'u takip edebilirsiniz.
Derslere istediğiniz zaman başlayıp istediğiniz zaman bırakabilirsiniz. Sınava hazırlanıyorsanız bu süreç boyunca yanınızda rehberlik edecek biri olması için ders almaya devam edebilirsiniz. Derslerinizin gününü ve saatini programınıza göre uydurabilirsiniz. Hangi yöntem başarılı olmanızı sağlayacaksa derslerinizi o yönteme uyarlayabilirsiniz!













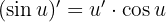
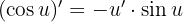
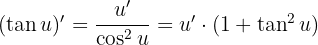
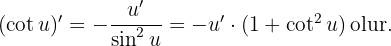




Güzel notlar. Çok iyi yaralandım teşekkürler!