Günlük koşturmacamız içinde matematiğin hayatımızın ne kadar derinlerine nüfuz ettiğini çoğu zaman fark etmeyiz. Alışverişten yemeğe, araba kullanmaktan problem çözmeye kadar pek çok alanda sayılar ve hesaplamalarla iç içeyiz. Peki, bu sayıları ifade etmek için kullandığımız semboller ve sistemler nasıl ortaya çıktı? İşte yazımızda, farklı eski medeniyetlerin geliştirdiği birbirinden ilginç sayı sistemlerine ve bu sistemlerin kendine has ifade biçimlerine doğru bir zaman yolculuğuna çıkıyoruz. Hadi başlayalım!
İnsanların yerleşik düzene geçmesiyle birlikte, ticaretin canlanması ve tarım arazilerinin ölçülüp hesaplanması gibi pratik ihtiyaçlar, matematiksel kavramların ve bunların yazılı olarak ifade edilmesinin önemini artırmıştır. İlk başlarda insanlar, çevrelerindeki nesnelerden ve doğadan ilham alarak basit semboller aracılığıyla sayıları ifade etmeye çalıştılar. Bir sayısını temsil etmek kolaydı, güneşi ya da Ay'ı bir sayısının temsili için kullanılıyordu. Yan yana iki göz ya da bir kuşun iki kanadı ikiyi, üç yapraklı yonca üçü, hayvan ayakları ise dördü temsil ediyordu. Bu ilk denemeler, sayısal düşüncenin somut dünyayla olan yakın bağını gözler önüne seriyor. Özel matematik desteği arayanlar, matematik özel ders ankara imkânlarından yararlanabilirler.
Antik Mısır'da devasa piramitlerin inşasında kullanılan hassas ölçümler ve hesaplamalar, onların onluk tabanlı ancak basamak değeri tam gelişmemiş sayı sistemleriyle nasıl mümkün oldu, hala tam olarak çözülememiş bir sırdır!
Antik Mısır medeniyeti ise sayıları ifade etmek için kendine özgü, görsel açıdan zengin bir sistem geliştirmiştir. "Hiyeroglif rakamlar"
Özellikle Antik Mısır’da kullanılan sembolik sistemler, bu zenginliğin en güçlü örneklerinden biridir.
Eski uygarlıkların kullandıkları sayı sistemleri içerisinden en önemlilerinden olan bu sistemde her bir sayı, bir nesnenin veya kavramın resmini temsil ediyordu. Tek birim için dikey bir çizgi kullanılırken, on birimi bir yay, yüz birimi kıvrımlı bir ip, bin birimi ise bir lotus çiçeği sembolize ediyordu. Büyük sayılar ise bu sembollerin yan yana getirilmesiyle oluşturuluyordu. Örneğin, dokuz sayısını yazmak için dokuz dikey çizgi kullanmak gerekiyordu. Mısırlıların kullandığı bu onluk tabanlı sistemin, muhtemelen ellerimizdeki on parmaktan esinlendiği düşünülmektedir. Bu sistemde sayılar, basamak değerine sahip olmasa da, pratik hesaplamalar ve kayıt tutma açısından önemli bir araçtı.
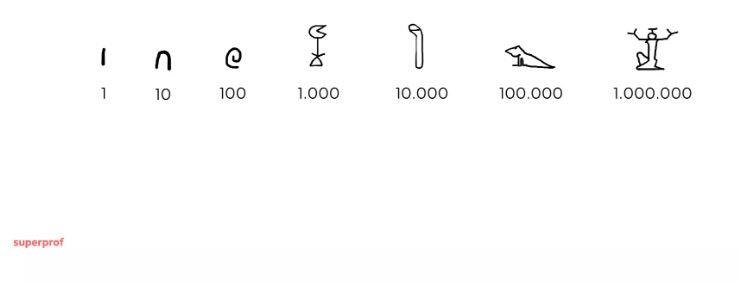

Eski Çin'deki Sayı Sistemleri
Eski Çin'deki matematik tarihini araştırmak ne yazık ki hiç de kolay değil. Qin Hanedanlığı sırasında, MÖ 213 civarında sayısız kitap ve belge kasıtlı olarak yok edildi. Bu nedenle, muhtemelen o zamana kadarki matematiksel kayıtların büyük bir kısmı kayboldu. Neyse ki, bazı insanlar kitapların içeriğini hatırlayabildi ve onları hafızalarından yeniden yazdılar. Bu nedenle, bilginin tam olarak hangi döneme ait olduğunu ve herhangi bir şeyin eklenip eklenmediğini veya değiştirilip değiştirilmediğini artık tam olarak anlamak mümkün değil. Ancak zaman zaman yapılan kazılarda, Eski Çin'deki matematik bilgisinin gelişimine dair çıkarımlar yapılmasına olanak tanıyan eserler bulunuyor. Henüz birkaç yıl önce bulunan Tsinghua Bambu Şeritleri, MÖ 480 ile 221 arasına tarihlendi ve 'en eski ondalık çarpım tablosu' olarak geniş çapta tanındı.
Basit işaretlerden doğan karmaşık düzen, insan aklının sonsuzluğunun kanıtıdır.
Bir Erken Dönem Çin Düşünürü
Yani Eski Çin'de de ondalık bir sistemle hesaplama ve sayma yapılıyordu. 1'den 9'a kadar rakamlar ve on kuvvetleri için adlandırmalar bulunmaktadır. Çok basamaklı bir sayı oluşturmak için, ilgili öğeler basitçe yan yana sıralanır. Bin sayısı, yüz sayısı, on sayısı, bir sayısı. Bugün bile Çin'de sayılar bu prensibe göre adlandırılmaktadır
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 100 | 1000 | 100.000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 | 百 | 千 | 万 |
| yī | èr | sān | sì | wǔ | liù | qī | bā | jiǔ | shí | bǎi | qiān | wàn |
Sümerlerin Sayı Sistemleri
Mezopotamya'nın kadim halklarından Sümerler, bölgede uzun süre hüküm sürmüş ve ardından Akadlar tarafından yerini Babil İmparatorluğu'na bırakmıştır. Ancak Sümerlerin bilimsel ve kültürel mirası, özellikle tekerleğin ve yazının (çeşitli bölgelerde eş zamanlı ortaya çıkmış olsa da) icadı gibi önemli başarıları sonraki medeniyetler tarafından da büyük değer görmüştür.
Sümerlerin kullandığı çivi yazısı, sıcak kil üzerine düz çizgilerle oluşturulduğu için kıvrımlı şekiller içermezdi ve bu özellik sayı sistemlerine de yansımıştır. Sümer sayı sistemi, şaşırtıcı bir şekilde, sadece iki temel sembol üzerine kuruluydu.
1 rakamı için bir işaret ve 10 rakamı içinse farklı bir işaret. Bu iki basit sembolün çeşitli kombinasyonları sayesinde, Sümerler 1'den 59'a kadar olan tüm sayıları etkili bir şekilde ifade edebiliyorlardı. Bu pratik ve özgün sistem, Mezopotamya'nın erken dönemlerindeki sayısal düşüncenin gücünü göstermektedir.

Altmışlık Sisteme Geçiş
Eski uygarlıkların kullandıkları sayı sistemleri içerisinde Sümer sayı sistemi çok önemli bir yer tutar. Bu sistemde 60 sayısına ulaşıldığında, yeni bir basamağa geçiliyordu. Bu yeni basamak, bir önceki basamağın soluna, aralarında hafif bir boşluk bırakılarak yazılıyordu. Sümerlerin sayı sistemini diğer birçok sistemden (modern onluk sistemimiz dahil) ayıran en temel özellik ise altmışlık tabanlı olmasıdır. Yani sayılar 10'un katları yerine 60'ın katları üzerinden ilerliyordu. Bu nedenle, örneğin 62 sayısını ifade etmek için, 60'lar basamağını temsil eden "1" sembolü ile 1'ler basamağını temsil eden "2" sembolü yan yana yazılırdı. Bu altmışlık sistem, Babiller tarafından da benimsenmiş ve astronomi ile zaman ölçümü gibi alanlarda kalıcı bir miras bırakmıştır.
| 60⁰ | 60¹ | 60² | 60³ |
|---|---|---|---|
| 1 | 60 | 3600 | 216.000 |

Orta Amerika'nın Gizemli Matematikçileri Mayalar
yılında kıyamet beklentisine yol açan bu takvim, aslında sonsuz bir zaman döngüsünü ifade eden matematiksel bir başyapıttır.
Mayaların sayı sistemi, diğer birçok antik kültüre kıyasla şaşırtıcı derecede basitti. Sadece bir nokta (1 için) ve bir çizgi (5 için) kullanarak tüm sayıları ifade edebiliyorlardı. Dahası, Mayalar sıfır kavramını da biliyor ve çok basamaklı sayılarda yer tutucu olarak kullanıyorlardı. Bu basit sembollerle karmaşık hesaplamalar yapabilmeleri, Maya matematiğinin ne kadar gelişmiş olduğunu göstermektedir. Ayrıca, kaliteli öğrenim için matematik özel ders fiyatları bilgilerini inceleyebilirsiniz.
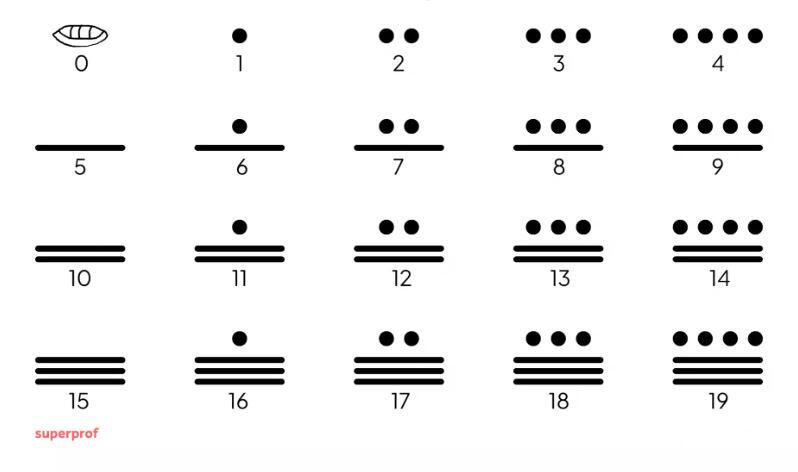
Maya sayı sisteminin ilginç bir özelliği, Çin sayma çubuklarındaki mantıkla benzer bir şekilde, 5 sayısının temel bir birim olarak kabul edilmesiydi. Bu durumun, insanların sayma işlemi için sıklıkla parmaklarını kullanmalarından kaynaklandığı düşünülmektedir. Nitekim onluk sistemin kökeni de genellikle iki eldeki on parmağa bağlanır. Ancak Mayalar, büyük olasılıkla ellerinin yanı sıra ayaklarındaki beşer parmağı da eşdeğer bir beşli birim olarak görmüşlerdir. Bu nedenle, Maya sayı sistemi 20 tabanlı bir sistemdir ve bu yüzden vigesimal sistem (yirmilik sistem) olarak adlandırılır. Bu durum, Maya matematiğinin insan anatomisiyle olan yakın ilişkisini göstermektedir.
| 20⁰ | 20¹ | 20² | 20³ | 20⁴ | 20⁵ |
|---|---|---|---|---|---|
| 1 | 20 | 400 | 8000 | 160.000 | 3.200.000 |
Mayalar, çok basamaklı sayıları yazarken ilginç bir yöntem izlerlerdi. Sayıları üst üste sıralarlardı. Bu sıralamada en küçük değer en altta bulunurdu. Bir Maya sayısını okumak ve kendi kullandığımız ondalık sisteme çevirmek için ise basit bir işlem uygulanırdı. En alttaki rakam 1 ile çarpılır, bir üstündeki rakam 20 ile çarpılır, onun da üstündeki rakam 20'nin karesi olan 400 ile çarpılır ve bu şekilde yukarı doğru devam edilirdi. Son olarak, elde edilen tüm bu çarpım sonuçları toplanarak Maya sayısının ondalık sistemdeki karşılığı bulunurdu. Bu dikey yazım şekli ve 20'lik tabanın kullanımı, Maya matematiğinin kendine özgü yapısını bir kez daha gözler önüne seriyor.
Roma’da gelişen Romen rakamları, sadeliğiyle dikkat çekerken hesaplama açısından sınırlıdır.
Antik Medeniyetlerin Sayısal Mirası
Farklı uygarlıkların sayı sistemlerini karşılaştırırken, Mayaların geliştirdiği matematiksel anlayış birçok açıdan öne çıkar.
İlk adımlarını Mezopotamya'nın verimli topraklarında atan, Antik Mısır'ın görkemli hiyerogliflerinde şekillenen, Doğu'nun kadim bilgeliğiyle Çin'de farklı bir boyut kazanan ve Orta Amerika'nın gizemli dehaları Mayaların özgün dünyasında bambaşka bir mantıkla karşımıza çıkan eski uygarlıkların sayı sistemleri, aslında insanlığın düşünce tarihinin de en çarpıcı aynalarından birini oluşturuyor.
Her bir medeniyet, kendi coğrafi koşulları, kültürel yapısı, ekonomik ihtiyaçları ve hatta felsefi yaklaşımları doğrultusunda, sayıları ifade etmek ve hesaplamalar yapmak için kendine özgü yöntemler geliştirmiştir. Sümerlerin altmışlık sistemi, karmaşık ticaret ağlarını ve astronomik gözlemlerini yönetmelerine olanak tanırken, Mısır'ın onluk tabanlı hiyeroglifleri, devasa yapıların inşası ve tarım arazilerinin ölçülmesinde pratik çözümler sunmuştur. Çin'in ondalık sistemi ve sayma çubuklarıyla gerçekleştirdiği hesaplamalar, ticari faaliyetlerin ve devlet yönetiminin etkinliğini artırmıştır. Uzak diyarlarda ise Mayalar, yirmilik sistemleri ve sıfır kavramına olan erken vakıflarıyla zamanın döngüsünü anlamaya ve evrenin sırlarını çözmeye odaklanmışlardır.

Eski uygarlıkların kullandıkları sayı sistemleri özelinde her bir sistem, kendi dönemi için son derece gelişmiş ve işlevsel araçlardı. Günümüzde kullandığımız onluk tabanlı modern sayı sistemi, bu zengin mirasın bir sentezi olarak varlığını sürdürmektedir. Babillerin altmışlık sisteminden miras kalan zaman ve açı ölçü birimleri, Maya takviminin matematiksel inceliği ve Çin'in pratik hesaplama yöntemleri, modern matematiğin temellerini oluşturan önemli kilometre taşlarıdır.
Bugün hala kullanılan 60 tabanlı sistem ise bu eski bilgilerin günümüze taşınan nadir örneklerindendir.
Gördüğümüz gibi, farklı eski uygarlıklar sadece farklı sayı sistemleri geliştirmekle kalmamış, aynı zamanda bu sayıları ifade etmek için kendilerine özgü matematik sembolleri ve sayı stilleri oluşturmuşlardır. Mezopotamya'nın çivi yazısından Mısır'ın hiyerogliflerine, Maya'nın nokta ve çizgilerinden Çin'in karmaşık karakterlerine kadar tüm sayı stilleri, o dönemin kültürel, teknolojik ve sanatsal özelliklerini yansıtmaktadır. Bu matematik sembolleri ve sayı stilleri ile tanışmak, sadece geçmiş uygarlıkların matematiksel yeteneklerini anlamamıza yardımcı olmakla kalmaz, aynı zamanda modern matematiksel notasyonun ve sembolizmin kökenlerine dair de önemli ipuçları sunar. Bu nedenle, antik dünyanın sayısal mirası, günümüz matematikçileri ve tarihçileri için hala büyüleyici bir araştırma alanı olmaya devam etmektedir.
Yapay zekâ ile özetle
























Ben çok beğendim proje ödevimi hepsini burdan yazdım . Bu yazıyı kim yazdıysa çok teşekkürler
Bence de gayet iyi
Abi ellerine sağlık
Çok iyi
Gerçekten kim yazdıysa yürekten alkışlıyorum çok yetenekli biri.e