Neden bir saatte 100 yerine 60 dakika olduğunu hiç düşündünüz mü? Ya da dairenin neden 360 dereceyi temsil ettiğini? Cevap, bizi milattan önceki binyıllara, antik Babil uygarlığına götürüyor. Günümüzde kol saatimize bakarken veya bir haritada koordinatları derece/dakika olarak okurken, aslında farkında olmadan Babillilerin mirasını kullanıyoruz.
Babil uygarlığı, sayıları yazmak ve hesaplamak için 60 tabanlı bir sistem kullandı. Peki neden özellikle 60? Bir teoriye göre Babilliler, parmaklarıyla 60'a kadar sayabiliyordu. Bir elin parmak boğumlarını sayarak 12'ye (baş parmağınızı kullanarak diğer dört parmağınızın 3'er boğumu) ulaşır, ardından diğer elin 5 parmağıyla bu 12'lik grupları sayarak 5×12 = 60 elde ederlerdi. Kulağa yaratıcı geliyor, değil mi? Günümüzün modern eğitim sisteminde benzer hesaplamaları öğrenirken, kaliteli matematik özel ders seçeneklerini değerlendirebilirsiniz.
Matematiksel açıdan bakınca, 60 sayısının çekiciliği bölenlerinde gizli. 60, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 gibi birçok sayıyla kalansız bölünebilir. Buna karşın bizim kullandığımız 10 tabanlı sistemde 10 sadece 2 ve 5’e tam bölünüyor. Babil sayı sistemi içinde 60 tabanı, özellikle kesirli hesaplarda büyük bir avantaj sağlıyordu. Örneğin 1/2, 1/3, 1/4, 1/5 veya 1/6 gibi kesirleri 60 tabanında kolayca tam sayılı olarak ifade edebiliyorlardı. Bu özellik, pazarda mal paylaşımından gökyüzünde zamanı ölçmeye kadar pek çok günlük durumda işlerini kolaylaştırdı. Kısacası, 60’ı seçmelerinin ardında hem pratik hem kültürel nedenler vardı. Parmaklarla saymanın getirdiği bir alışkanlık ve 60’ın “her şeye bölünebilen” yapısı.
Modern hesaplama sistemlerinin kökenine inildiğinde, Mayaların geliştirdiği matematiksel yöntemlerle bu kadim sistemler arasında birçok benzerlik bulunabilir.


Sistem Nasıl Çalışıyordu?
Babil sayı sistemi ilk bakışta karmaşık görünebilir, ancak aslında oldukça zekice tasarlanmıştı. Bizim onluk sistemimizde 0-9 arası on farklı rakam yani matematik işaretleri varken, Babilliler 60 tabanlı sistem için sadece iki temel sembol kullandılar!
Bir “birim” çivi işareti (dikey bir kama izi, kabaca | şeklinde) 1 değerindeydi;
bir “onluk” çivi işareti (açılı yatay bir kama izi, kabaca < şeklinde) ise 10 değerindeydi.
Bu iki sembolü tekrar ederek veya yan yana getirerek 1'den 59'a kadarki tüm sayıları yazabiliyorlardı. Örneğin, 1 için |, 2 için ||, ... 9 için ||||||||| (dokuz tane |), 10 için <, 20 için << gibi. 37 yazmak için <<<||||||| (üç adet < yanına yedi adet |) kullanılırdı.
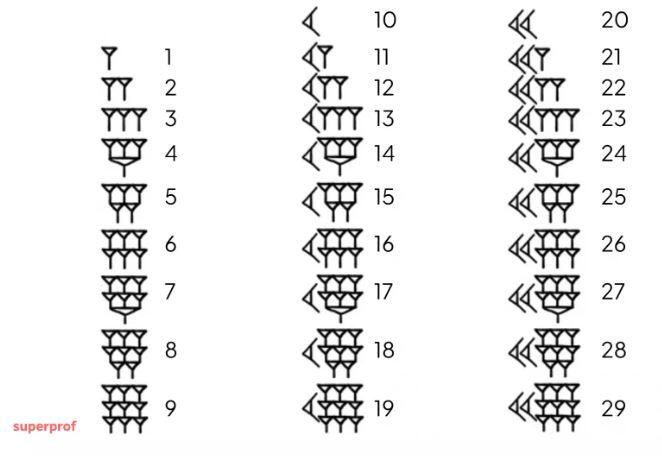
Babillilerin sistemi pozisyonel (basamak değerli) bir yapıdaydı. Yani bir sembolün değeri, bulunduğu konuma göre değişiyordu. Tıpkı bizim 123 sayımızda sol baştaki 1'in “yüz” anlamına gelmesi gibi, Babil’de de sağdaki sütun 1–59 arası birler, onun solu 60×(1–59) arası 60’lar, daha solu 60^2’ler (3600’ler) şeklindeydi. Örneğin Babilliler bir sayıyı tablette 2 boşluk 15 şeklinde (iki grup sembol aralarına boşluk bırakarak) yazmışsa, bu 2×60 + 15, yani 135 anlamına gelirdi.
Bu noktada modern bakışla Babil sayı sistemi içinde “Eksik bir şey yok mu?” diye sorabiliriz. Evet, 0 (sıfır) kavramı başlangıçta yoktu. Babilliler ilk başta herhangi bir sıfır sembolü kullanmadılar. Bir basamak boşsa, onu sadece boş bıraktılar veya diğer sembollerden biraz ayırdılar. Örneğin sadece tek bir | işareti, bağlama göre 1 de 60 da anlamına gelebiliyordu! (Bu durumda sayının ne olduğu cümlenin veya hesabın bağlamından anlaşılmak zorundaydı.) Bu durum bize belirsiz görünse de, Babilliler yüzyıllarca büyük bir sorun yaşamadan bu şekilde idare ettiler. Yine de, M.Ö. 300’lere gelindiğinde, ilerleyen Babil döneminde bu boşluğu göstermek için çivi yazısında iki eğik kama gibi bir işaret kullanmaya başladılar. Bu işaret bir sayının ortasında “boş basamak” anlamına geliyordu (bir nevi sıfırın habercisi diyebiliriz), ancak sayının sonunda kullanılmadığı için tam bir sıfır konsepti değildi. Gerçek sıfır sayısını icat etmek M.Ö. 1. yüzyılda Hintli matematikçilere kısmet olacaktı.
fazla matematik tableti bulunmuştur.
Özetle, Babilliler konumsal değer fikrini (basamak değeri sistemi) geliştiren ilk uygarlıklardan biriydi. Sadece iki sembolle 60 tabanlı bir sistemi yazabilmeleri ve işlemleri yapabilmeleri, dönemine göre muazzam bir yenilikti. Bu sistem, kendilerinden sonra gelen Yunan ve Romalıların sayı sistemlerine göre çok daha gelişmişti (Romalılar hala harf benzeri rakamlarla, pozisyonel olmayan bir sistem kullanıyordu). Babil sayı sistemi, matematik tarihinde adeta bir dönüm noktası oldu.
Babil rahipleri, Ay’ın kızıl renge büründüğü anlarda bunun sadece gökbilimsel bir olay değil, aynı zamanda tanrıların bir mesajı olduğuna inanırlardı. Ay tutulması genellikle krallık için kötü bir alamet sayılırdı. Hatta bazı durumlarda, tutulma sırasında kralın yerine “sahte bir kral” atanır, gerçek kral saklanırdı. Bu kişi birkaç gün “kral” gibi yaşar ama tutulmanın ardından çoğu zaman kurban edilirdi. Gerçek kral ise “lanetten kurtulmuş” sayılırdı!
Astronomi, Takvim ve Mimarlıkta Babil Matematiğinin Etkileri
Babil matematiğinin gücü, sadece soyut hesaplarda değil, günlük yaşam ve bilimsel çalışmalarda da ortaya çıkıyordu. Babilliler, dönemin şartlarında inanılmaz sayılabilecek ilerlemeler kaydetmiş ve bu sayede astronomiden takvim yapımına, mimarlıktan mühendisliğe birçok alanda kalıcı etkiler bırakmıştır.
Babil uygarlığı belki de en çok astronomi gözlemleri ve kayıtlarıyla tanınır. Geceleri zigurat denilen kulelerin tepesinde yıldızları izleyen rahip-astronomlar, gök hareketlerini anlamak için yoğun bir çaba içindeydi. İşte burada 60 tabanlı matematik onlara hizmet etti. Babilliler gökyüzünü bugün kullandığımız gibi 360 dereceye böldüler ve ekliptik düzlem üzerinde 12 takımyıldızlık (burçluk) bir zodyak sistemi oluşturdular. 360 sayısını seçmeleri rastgele değildi: Bir yılın yaklaşık 360 gün olması fikri ve 60’ın katı oluşu bunda etkili olmuş olabilir. Böylece her bir burç dilimi 30 derece olarak tanımlandı. Bu sistem günümüzde hala kullanılıyor; astrolojideki 12 burç konsepti ve her dairenin 360 derece oluşu Babillilere dayanıyor desek yanlış olmaz. Bu alanda meraklıysanız, matematik özel ders ankara seçeneklerini inceleyebilirsiniz.
Babilli astronomlar, sadece yıldızların konumunu belirlemekle kalmadı, aynı zamanda gezegen ve Ay hareketlerini hesaplamada ustalaştılar. Örneğin, Ay ve Güneş tutulmalarının tekrarını yaklaşık 18 yıl 11 gün süren Saros döngüsüyle ilişkilendirmişlerdi. Bu sayede tutulmaların ne zaman olacağını önceden tahmin edebiliyorlardı. Ayrıca gözlemledikleri 5 gezegenin (Merkür, Venüs, Mars, Jüpiter, Satürn) hareketlerini kaydeden ayrıntılı astronomi günlükleri (tabletleri) oluşturmuşlardı. Babillilerin geliştirdiği bu gök günlükleri ve hesaplama yöntemleri, daha sonraki Yunan astronomlarına da temel oldu. Hatta yakın zamanda yapılan bir keşif, Babilli rahiplerin Jüpiter’in konumunu hesaplamak için geometrik bir yöntem kullandığını ortaya çıkardı – bu yöntem kabaca alan hesabına dayalıydı ve benzeri teknikler ancak 1500 yıl sonra Avrupa’da gelişecekti. Kısacası, Babilliler gökleri hesaplarken zamanının çok ötesinde matematiksel yaklaşımlar benimsediler.
Zaman ölçümüne dair ilginç örnekler, antik dünyanın sayı sistemleri üzerine çalışan topluluklarda da görülür.
Babillilerin matematiği, takvim yapımında da belirleyici rol oynadı. Babil takvimi temelde Ay yılına dayanıyordu. Bir yıl, yaklaşık 29.5 günlük 12 aydan oluşuyordu. Bu da 354 gün yapar, ki güneş yılından 11 gün eksiktir. Babilliler, birkaç yılda bir (yaklaşık 3 yılda bir) 13. ayı ekleyerek takvimlerini mevsimlerle uyumlu hale getirmeyi başardılar. Böylece tarım ve bayram zamanlarını şaşırmıyorlardı. Bir Babil yılı genellikle 12 ay (bazı yıllar 13 ay) sürdüğü için, 19 yıllık döngülerde ay takvimi ile güneş takvimi uyumlu hale getiriliyordu (daha sonra Meton döngüsü olarak bilinen sistem).
Takvim konusundaki belki de en ilginç mirasları, haftanın 7 gün olması kavramıdır. Babilliler, gökyüzünde çıplak gözle görülen 7 önemli gök cismine büyük önem veriyorlardı: Güneş, Ay ve 5 gezegen. Ay’ın yaklaşık 28 günde bir döngüsünü tamamladığını gözlemlemişler ve bu döngüyü dörder haftalık periyotlara ayırmışlardı. Her bir 7 günlük periyot, bir nevi “hafta” olarak kullanıldı. Haftanın her bir gününü de bu gök cisimlerine atfettiler. Örneğin, 7. gün Ay tanrısına, bir diğer gün Venüs’e (İştar’a) adanmıştı.
Bugün kullandığımız 7 günlük hafta düzeni ve bazı dillerdeki gün adları doğrudan doğruya bu Babil uygulamasından etkilenmiştir. (Örneğin İngilizcede Saturday = Satürn’ün günü, Monday = Ay’ın günü gibi adlandırmalar, Babillerden Romalılara geçen geleneğin ürünüdür.) Babilliler ayrıca her ayın 7, 14, 21 ve 28. günlerini özel kabul eder, belki de yarı-dinlenme günleri olarak ayırırlardı. Bu, daha sonra farklı kültürlerde dini veya tatil anlamı kazanan haftalık döngünün başlangıcıydı diyebiliriz.
Aynı şekilde, Antik Mısır’daki sayı stilleri, sembolik sistemler ve yazı diliyle iç içe geçmiş biçimde gelişmiştir.

Babiller Hakkında Az Bilinenler
Babilliler sıfır rakamını kullanmıyorlardı. Sayılar arasında boşluk bırakarak anlamsal bir sıfır hissi verseler de, gerçek sıfır kavramı M.Ö. 1. yüzyılda Hindistan’da icat edildi. Yani Babillilerin hiçbir zaman “0” diye bir sayısı olmadı!
YBC 7289 adlı Babil tabletinde,

(2’nin karekökü) değeri 1;24,51,10 biçiminde 60’lık sistemle kaydedilmiş. Bu, ondalık sistemde 1.41421296... anlamına geliyor ki gerçek 1.41421356... değerine inanılmaz yakın – neredeyse 6 basamaklı doğrulukta! Babilliler, bir karenin köşegen uzunluğunu bu yöntemle hesaplayarak tarihin ilk yüksek hassasiyetli hesaplarından birini yapmışlar.
Rakam sembolleri üzerine düşünürken, Romen rakamlarının nasıl öğrenileceği konusunda şaşırtıcı detaylara rastlayabilirsin.
Matematik, yalnızca sayıların değil, evrenin de dilidir.
Galileo Galilei
Babilliler dairenin çevresini hesaplarken π (pi) için genelde 3 değerini kullandılar. Bazı tabletlerde π ≈ 3 + 1/8 = 3.125 olarak geçiyor. Bu, gerçek π (3.1416...) için fena bir yaklaşım sayılmaz. Aynı dönemde Mısırlılar 3.16 değerini kullanıyordu; Babillilerin 3 veya 3.125 seçimi, hesaplarının biraz daha basit kalmasını sağlıyordu.
Çarpım tablosu ezberlemek zor geliyorsa, Babilli bir matematikçi size şu dahiyane fikri verirdi.
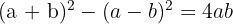
Gerçekten de onlar, 1'den 59'a kadar sayıların karelerini gösteren tabletler kullanarak bu formül sayesinde çarpmaları yapabiliyordu. Yani iki sayıyı çarpmak için, toplamları ile farkının karelerini alıp çıkarıyorlar, sonra dörde bölüyorlardı! Ek olarak, günümüzde eğitimde tercih edilen matematik özel ders fiyatları hakkında bilgi alabilirsiniz.
Yapay zekâ ile özetle
















Kesinlikle faydali ve çok işe yarar bir yazı olmuş! 🤗