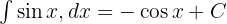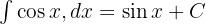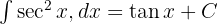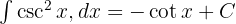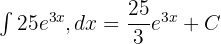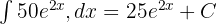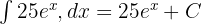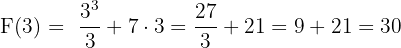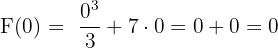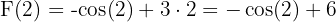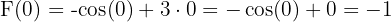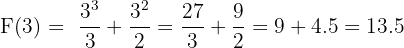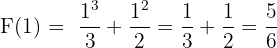Fonksiyonun belirli integrali, bir fonksiyonun belirsiz integrali ve ters türevi ile yakından alakalıdır. Temel fark şu: Fonksiyonun belirsiz integrali varsa bunun bir gerçek sayı değeri vardır. Belirli bir integralin ise başlangıç ve bitiş değerleri vardır. Bu da [a, b] kapalı bir aralık olduğu anlamına gelir.
İntegral kavramı ilk olarak 17. yüzyılda Gottfried Wilhelm Leibniz tarafından tanımlandı. İntegral, Latince "toplam" kelimesinin ("ſumma", "summa") baş harfi s'nin biraz evrim geçirmiş hâliyle, ∫ işareti ile gösterilir.
Belirli bir aralıkta integral sembolünün üstünde ve altında [a, b] aralığının sınırları vardır. Bu sayılar a ve b x-değerlerini temsil eder. İntegral limitleri olarak da bilinirler.
Belirli integral tanımındaki integral sembolü, bir fonksiyonun ters türevini belirtmek için belirsiz integral sembolüne benzer. Fonksiyonların belirli ve belirsiz integrallerini temsil eden semboller birbirine benzer görünse de her iki kavram da birbirinden farklıdır. Belirli bir integral bir sayıdır, oysa belirsiz bir integral bir fonksiyonlar grubudur.
Matematikte İntegral Türleri
Matematikte iki tür integralin ne olduğuna bir bakalım. İki tür integral vardır:
- Belirli integral
- Belirsiz integral
Belirli İntegral
Üst ve alt sınırları olan bir integral, belirli olarak bilinir.
Belirli bir integral şu şekilde gösterilir:
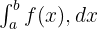
Belirsiz İntegral
Üst ve alt limit içermeyen integral, belirsiz integral olarak bilinir.
Belirsiz bir integral şu şekilde temsil edilir:
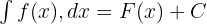
Burada C bir sabittir ve f(x) fonksiyonu bir tamsayı olarak bilinir.
Belirli İntegral
Bir fonksiyon, f(x) ve kapalı bir aralık [a, b] verildiğinde, belirli integral , f(x) grafiği, x ekseni ve x = a ve x = b dikey çizgileri tarafından sınırlanan alanı temsil eder.
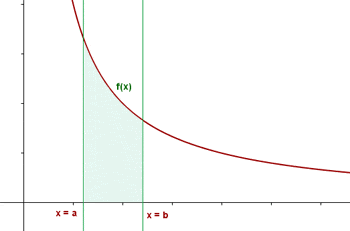
Belirli integral, 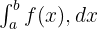şeklinde gösterilir.
Burada:
∫, integral işaretidir.
a, entegrasyonun alt sınırıdır.
b, entegrasyonun üst sınırıdır.
f(x), integraldir.
dx, x'in diferansiyelidir ve integrali alınacak fonksiyonun değişkenini gösterir.
Belirli İntegralin Özellikleri
Belirli integrallerin bazı özelliklerinden bahsedelim.
Ters Aralık
Belirli integralin değerinin işareti, integralin sınırları değiştirildiğinde değişir. Matematiksel olarak, bu özellik şu şekilde yazılabilir:
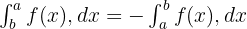
Sıfır Genişlik
İntegrasyon limitleri aynı ise belirli integral sıfırdır. Matematiksel olarak, bu özelliği şu şekilde gösterebiliriz:
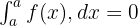
Aralık Ekleme
Eğer c , [a, b] kapalı aralığı içindeki bir nokta ise, o zaman belirli integrali [a, c] ve [c, b] kapalı aralıklarındaki iki integralin toplamı olarak parçalara ayırırız. Bu özelliği matematiksel olarak şu şekilde yazabiliriz:
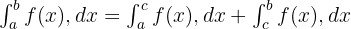
Toplam/Fark
Fonksiyonların toplamının veya farkının belirli integrali, integrallerin toplamına veya farkına eşittir. Matematiksel olarak şu şekilde yazabiliriz:
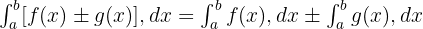
Sabit Çoklu
Bir fonksiyonla çarpılan sabitin integrali, sabit ile fonksiyonun integralinin çarpımına eşittir. Matematiksel olarak şu şekilde yazabiliriz:
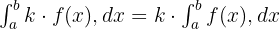
İntegral Kuralları
Bir Sabitin İntegrali:
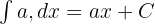
Sabit ile Çarpma:
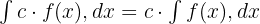
Kuvvet Kuralı:
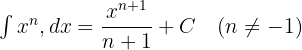
Toplam/ Fark Kuralı:
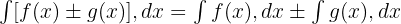
Trigonometrik İntegraller
Trigonometrik fonksiyonların önemli integrallerinden bazıları şöyledir:
İntegral Alma Kuralları
1. Değişken Değiştirme Yöntemi
∫ f(x)dx integrali ∫ g(u). u’du şeklinde yazıldığında bilinen integral formüllerinde birine dönüşüyorsa değişken değiştirme yöntemi kullanılır. Burada u; x’in bir fonksiyonudur.
Şöyle örnekleyelim:
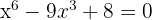
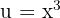diyelim. Bu durumda denklem:
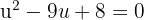
Bu denklemi çözelim:
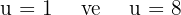
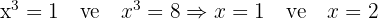
2. Kısmi İntegrasyon Yöntemi
Örneğin:
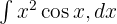integralinin sonucunu bulalım.
Kısmi integrasyon yöntemini kullanalım:
Kısmi integrasyon formülü:
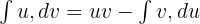
Bu formülü uygulayalım:
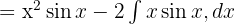
Bir Fonksiyonun İntegralini Hesaplama Adımları
Verilen fonksiyonun integralini hesaplamak için aşağıdaki adımları izleyebiliriz:
Adım 1 - Fonksiyonun ters türevini hesaplayın
Adım 2 - Fonksiyonun ters türevindeki değerleri (üst ve alt limitler) değiştirin
Adım 3 - Farkı alın ve cevabı sadeleştirin
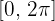aralığında 
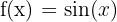fonksiyonunun belirli integralini hesaplayalım.
- Adım 1:
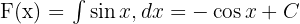
- Adım 2:
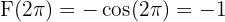
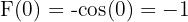
- Adım 3:
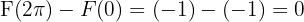
Örnekler
Şimdi de verilen fonksiyonların belirli ve belirsiz integrallerini hesaplayacağımız birkaç örnek çözelim.
Örnek 1
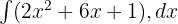integralini hesaplayın.
Çözüm 1
İlk adımda, toplama/çıkarma veya sabitlerle çarpma gibi belirli integral kurallarını kullanarak integralleri parçalara ayırıyoruz. Bu kuralları kullanarak yukarıdaki işlevi şu şekilde yeniden yazabiliriz:
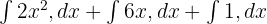
Bir sonraki adımda, aşağıdaki gibi integral işaretlerinden önceki sabitleri kaydıracağız:
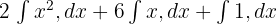
İntegrallerin kuvvet kuralını hatırlayın:
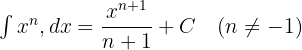
Bu kuralı, yukarıdaki polinomun sabit teriminin integralini bulmak için kuvvetlerin ve integral sabit kuralının integrallerini hesaplamada kullanacağız:
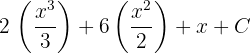
Son adımda, son cevabı şu şekilde en basitleştirilmiş hâliyle yazabiliriz:
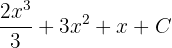
Örnek 2
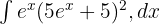
Çözüm 2
- İfadeyi Genişletme:
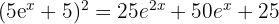
Bu durumda integral: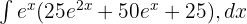
- İntegrali Parçalara Ayırma:
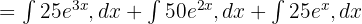
- Her Terimin İntegralini Hesaplama:
- Sonuç:
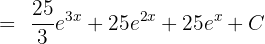
Örnek 3
Aşağıdaki fonksiyonun belirli integralini bulun:
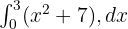
Çözüm 3
- Belirsiz İntegrali Bulma (Ters Türev):
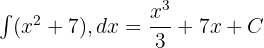
- Belirli İntegrali Hesaplama:
Belirli integral formülü: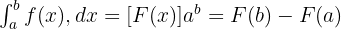
Bu durumda:
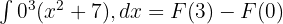
Ters Türevde Değerleri Yerine Koyma:
Sonucu Hesaplama: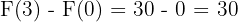
Örnek 4
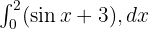
Çözüm 4
- Ters Türevi Bulma:
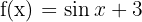fonksiyonunun ters türevi: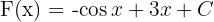
- Belirli İntegral Formülü:
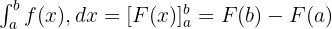
- Ters Türevde Değerleri Yerine Koyma:
- Sonuç:
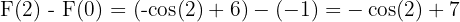
Örnek 5
Aşağıdaki fonksiyonun belirli integralini bulun:
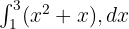
Çözüm 5
- Belirsiz İntegrali Bulma (Ters Türev):
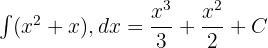
- Belirli İntegral Formülü:
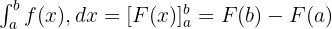
- Ters Türevde Değerleri Yerine Koyma:
- Sonucu Hesaplama:
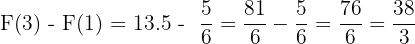
Özel Derslerle İntegral
Neden mi özel dersler almayı bir düşünün deriz? Hemen açıklayalım.
- Özel öğretmenler sizin hızınıza göre ilerler. Özel öğretmen seçerken göz önünde bulundurmanız gereken en önemli faktör muhtemelen budur. Sınıfın gerisinde kalma gibi bir derdiniz olmaz. Ya da zaten bildiğiniz konularla fazla zaman kaybetmezsiniz.
- Özel ders öğretmeniniz sadece sizinle ilgilenir. Kendi tercih ettiğiniz öğrenme tarzı için hangi öğretmenin doğru olduğuna karar vermenize yardımcı olacağından, özel ders almayı düşünüyorsanız öncesinde hangi öğrenim yöntemlerinin size uygun olduğunu bir düşünün. Öğretmeninizin ilgisi sadece sizde olacağından çok daha hızlı ilerleme kaydedebilirsiniz.
- Özel ders öğretmeniniz, önünüzdeki engelleri aşmanızı sağlayabilir. Belli bir noktada takıldığınızda öğretmeniniz size yardımcı olur ve çok zaman kaybetmeden ilerlemenize devam edersiniz. Özel ders öğretmeninize aklınıza takılan her şeyi sorarsınız, böylece yanınızda size her zaman rehberlik edecek biri olur. İntegrale çalışmak istiyorsanız sadece ona odaklanırsınız. Matematiği baştan sona yeniden öğrenmek istiyorsanız derslerinizi ona göre programlarsınız. Karar sizde.
- Özel dersler son derece esnek olur. Superprof gibi online ders platformları sayesinde evinizin rahatlığını bırakmadan özel dersler alabilirsiniz. Nereye giderseniz gidin, derslerinize ara vermenize gerek kalmaz. İnternet bağlantınız ve teknolojik bir cihazınız olduğu sürece her an her yerde eğitiminize devam edebilirsiniz.
- Özel derslerle en iyi kaynaklara erişebilirsiniz. Öğretmeniniz eğer deneyimli biriyse sizin için en doğru kaynakları söyleyecektir. Böylece siz binlerce kaynak arasından seçim yapmaya çalışmazsınız. Anlamadığınız yerlerde size videolar, online siteler vb. söyleyerek konuya farklı bir açıdan bakmanızı sağlar.
Üstelik Superprof'ta çoğu öğretmen ilk dersini ücretsiz sunuyor. Bizce denemeye değer!
İntegral ve türevin karmaşık dünyasında kendinizi kaybetmek yerine bir profesyonelden özel dersler alarak işin özüne inebilirsiniz. Ya da bu konuda iyi olan bir üniversite öğrencisinden de dersler alabilirsiniz. Belki de yaşıtlarınızdan dinleyince daha kolay anlarsınız. Online dersler, yüz yüze ve bire bir dersler, grup dersleri… Tarzınıza, programınıza ve bütçenize en çok hangi özel ders türü uyuyorsa kısa bir araştırmayla sizin için faydalı olabilecek öğretmenleri hemen bulabilirsiniz. Matematik özel ders ve matematik özel ders Ankara seçenekleriniz Superprof'ta oldukça geniş!
Bu yazıyı beğendiniz mi? Puanlayın!
Loading...
