Matematik deyince bazen gözümüz korkabilir, kabul edelim. Ama analitik geometri, matematiğin o soğuk yüzünü biraz olsun ısıtan, daha "insancıl" bir dalı sanki. Geometriyle cebiri öyle güzel bir araya getiriyor ki, şekilleri ve konumları sayılarla, denklemlerle anlatabiliyoruz. Yani, bir üçgeni, bir daireyi, hatta karmaşık eğrileri bile matematiksel bir dille ifade edebiliyoruz! Bu müthiş fikir, 17. yüzyılda Descartes ve Fermat gibi dahiler sayesinde doğdu. O günden beri de bilimden mühendisliğe, oyun dünyasından navigasyona kadar hayatımızın her alanında bize yol gösteriyor.
Bu yazıda, analitik geometrinin en temel formüllerine ve kavramlarına şöyle yakından bakacağız. Doğru denklemlerini çözmeye çalışacak, noktalar arasındaki mesafeleri kolayca bulmanın yollarını keşfedecek, farklı farklı eğri türlerini tanıyacak ve geometrik şekilleri nasıl dönüştürebileceğimizi öğreneceğiz. Yani, matematiğin bu keyifli dünyasında beraberce bir yolculuğa çıkacağız! Analitik geometri formülleri yazımıza, analitik geometrinin evi olan koordinat sistemi ile başlayacağız elbette!
Geometri hakkında kapsamlı bir rehber için linkteki yazımızı mutlaka oku!
Koordinat Sistemi
Analitik geometrinin olmazsa olmazı, o meşhur koordinat sistemi! Genelde kullandığımız Kartezyen koordinat sistemi, iki dik eksenden oluşuyor: x-ekseni (yatay olan) ve y-ekseni (dikey olan). Düzlemdeki herhangi bir noktayı, bu eksenlere göre bir sayı çiftiyle (x, y) gösterebiliyoruz. Bu sayılara da o noktanın koordinatları diyoruz. Mesela, (3, 5) noktası, x-ekseninde 3 birim, y-ekseninde 5 birim ileride demek oluyor.
Nokta
Düzlemdeki bir yer, koordinat sistemi sayesinde bir nokta ile temsil ediliyor. Her noktanın kendine özel bir "adresi" var, o da koordinatları işte.
Doğru
İki noktayı birleştiren en kısa çizgiye doğru diyoruz. Doğruların da kendine has denklemleri var, onları da öğreneceğiz.
Eğri
Düzlemde noktaların oluşturduğu o akıcı, kıvrımlı çizgilere eğri diyoruz. Çember, parabol, elips gibi farklı eğri türleri var ve bunların da denklemleriyle uğraşacağız.
Bu temel kavramlar, analitik geometrinin alfabesi gibi bir şey. Bunları kavradıktan sonra, daha karmaşık konuları anlamak da kolaylaşacak. Şimdi hazırsanız, doğruların denklemlerini inceleyelim.
Analitik geometride doğrular, en temel ve en çok karşılaşılan geometrik şekillerden biridir. Bir doğrunun ne kadar önemli olduğunu düşünsenize: iki nokta arasındaki en kısa yolu temsil eder, birçok şeklin kenarını oluşturur ve günlük hayatta da karşımıza sıkça çıkar (örneğin, bir yol, bir cetvelin kenarı). Şimdi gelin, doğruların matematiksel dünyasına biraz daha yakından bakalım ve onları denklemlerle nasıl ifade edebileceğimizi keşfedelim.
Bu form, bir doğrunun eğimini (m) ve y-eksenini kestiği noktayı (n) açıkça gösteren bir denklemi ifade eder. "m" değeri, doğrunun ne kadar dik olduğunu (eğimini) belirtir. Pozitif "m" değeri, doğrunun sağa doğru yükseldiğini, negatif "m" değeri ise sağa doğru alçaldığını gösterir. "n" değeri ise doğrunun y-eksenini hangi noktada kestiğini gösterir. Aynı zamanda bu form, doğrunun grafiğini çizmeyi ve eğimini/y-kesim noktasını belirlemeyi kolaylaştırır.
Hadi daha somut bir örnekle açıklayalım.
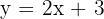
doğrusu, eğimi 2 olan, x eksenini (-2) noktasında ve y-eksenini 3 noktasında kesen bir doğrudur.
Nokta-Eğim Formu
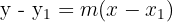
Bu form ise bir doğrunun eğimini (m) ve üzerindeki belirli bir noktayı (x1,y1) kullanarak denklemi oluşturmayı sağlar. Eğer bir doğrunun eğimini ve üzerindeki bir noktayı biliyorsak, bu formülü kullanarak doğrunun denklemini kolayca yazabiliriz.
Örneğin eğimi (-1) olan ve (1, 4) noktasından geçen doğrunun denklemi şu şekilde olur.
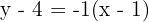
İki Nokta Formu
Eğer bir doğrunun üzerindeki iki farklı noktayı (x1,y1) ve (x2,y2) biliyorsak, bu iki noktayı kullanarak doğrunun denklemini oluşturabiliriz. Bu form, nokta-eğim formülünden türetilebilir.
Genel Form (Ax+By+C=0) şeklinde olacaktır.
Örneğin 3x−2y+6=0 bir doğru denklemidir.
Bu form, bir doğrunun denklemini en genel haliyle ifade eder. A, B ve C, sabit sayılardır. Bu form, doğruların birbirlerine göre konumlarını (paralel, kesişen, çakışık) belirlemek için kullanışlıdır.
Etkili Geometri Çalışma Tekniklerini merak ediyor musun?
Doğruların Birbirlerine Göre Durumları
İki doğru, bir düzlemde üç farklı durumda olabilir.
- Paralel Doğrular: Eğimleri eşit olan doğrular paraleldir. Yani, m1=m2 ise doğrular paraleldir.
- Kesişen Doğrular: Eğimleri farklı olan doğrular bir noktada kesişir. Yani, m1, m2'ye eşit değilse doğrular kesişir.
- Çakışık Doğrular: Aslında aynı doğruyu temsil eden doğrular çakışıktır. Denklemleri orantılıdır
Doğru Denklemleri ve Özellikleri
Doğru denklemlerinin derinliklerine iniyoruz şimdi.
Bir doğrunun x-ekseni ile pozitif yönde yaptığı açıya eğim açısı denir. Eğim açısının tanjantı, doğrunun eğimine eşittir.
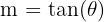
Burada m doğrunun eğimini, θ ise eğim açısını temsil eder.
İki doğrunun kesişmesiyle oluşan açılar, doğruların eğimleri kullanılarak hesaplanabilir.
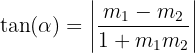
Burada ise α doğrular arasındaki açıyı, m1 ve m2 ise doğruların eğimlerini temsil eder.
Nokta ve Doğru İlişkisi
Bir noktanın bir doğruya olan uzaklığı, noktadan doğruya çizilen dikmenin uzunluğuna eşittir.
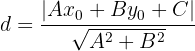
Burada (x0,y0) noktanın koordinatlarını, Ax+By+C=0 ise doğrunun genel denklemini temsil eder.
Örneğin (2, 3) noktasının 4x - 3y + 5 = 0 doğrusuna uzaklığını hesaplayalım.
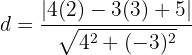
d=4/5
İki Nokta Arası Uzaklık
İki nokta arası uzaklık formülü ise şu şekilde.
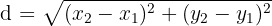
d: İki nokta arasındaki uzaklık
(x₁, y₁): Birinci noktanın koordinatları
(x₂, y₂): İkinci noktanın koordinatları
TYT Geometri için kapsamlı bir rehber hazırladık, linke tıkla!
Eğri Denklemleri
Eğriler, analitik geometrinin önemli bir parçasıdır. Doğrusal olmayan şekilleri temsil ederler ve denklemleri, noktaların belirli bir kurala göre hareket etmesiyle oluşur.
Çember: Bir noktaya eşit uzaklıktaki noktaların kümesidir. Merkezi (h, k) ve yarıçapı r olan çemberin denklemi:
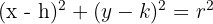
Parabol: Bir noktaya (odak) ve bir doğruya (doğrultman) eşit uzaklıktaki noktaların kümesidir.
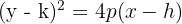
Burada (h, k) tepe noktası ve p odak ile doğrultman arasındaki mesafedir.
Elips: İki noktaya (odaklar) uzaklıkları toplamı sabit olan noktaların kümesidir.
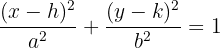
Burada ise (h, k) merkez, a yatay yarıçap ve b dikey yarıçaptır.
Hiperbol: İki noktaya (odaklar) uzaklıkları farkı sabit olan noktaların kümesidir.
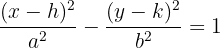
Burada (h, k) merkezdir.
Geometrik Dönüşümler
Geometrik dönüşümler, bir şeklin konumunu, boyutunu veya yönünü değiştiren işlemlerdir. Analitik geometri, bu dönüşümleri matematiksel olarak ifade etmemizi ve uygulamamızı sağlar. İşte bazı temel geometrik dönüşümler:
- Öteleme: Bir şeklin koordinat sisteminde belirli bir vektör doğrultusunda kaydırılması işlemidir. Her nokta aynı miktarda ve aynı yönde hareket eder.
- (x, y) noktasının (h, k) vektörü ile ötelenmesi
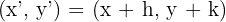
- Dönme: Bir şeklin bir nokta (genellikle orijin) etrafında belirli bir açı kadar döndürülmesi işlemidir.
- (x, y) noktasının orijin etrafında θ açısı kadar döndürülmesi aşağıdaki formüller ifade edilir.
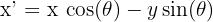
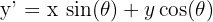
- Yansıma: Bir şeklin bir doğruya göre simetriğinin alınması işlemidir. Şeklin her noktası, yansıma doğrusuna eşit uzaklıkta olacak şekilde karşı tarafa taşınır.
- x-eksenine göre yansımayı nasıl yazarız?
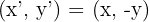
- y-eksenine göre yansıma aşağıdaki gibi olacaktır.
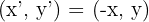
- Ölçekleme: Bir şeklin boyutunun belirli bir oranda büyütülmesi veya küçültülmesi işlemidir.
- (x, y) noktasının x ve y eksenlerinde sırasıyla a ve b oranlarında ölçeklenmesi ise aşağıdaki şekildedir.
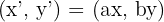
Matematik ve Görselliğin Buluşması
Analitik geometri, matematiğin soyut dünyası ile görsel dünyanın bir araya geldiği önemli bir alan. Denklemler aracılığıyla şekilleri ifade etmemizi, temel açı çeşitlerini geometrik problemleri cebirsel yöntemlerle çözmemizi ve uzaydaki nesneleri manipüle etmemizi sağlıyor. Şimdi şöyle lise yıllarınıza gidin ve analitik geometriyle ilk tanıştığınız zamana dönün. Bu ders benim günlük hayatta ne işime yarayacak diye düşündüğünüz olmuştur belki de...
Bilgisayar grafikleri, oyun geliştirme, mühendislik, fizik ve daha birçok alanda analitik geometriye dayalı kavramlar ve algoritmalar kullanılır. Örneğin, bir bilgisayar oyununda bir karakterin hareketleri, bir binanın tasarımı veya bir robotun navigasyonu, analitik geometri prensipleri kullanılarak gerçekleştirilir. İşte analitik geometrinin işe yaradığı alanlardan birkaçı.
Yaratıcılığımızın Pusulası
Analitik geometri, sadece matematiksel formüller ve denklemler sunmakla kalmaz, aynı zamanda yaratıcılığımızı harekete geçiren, hayallerimizi gerçeğe dönüştürmemize yardımcı olan çok yönlü bir pusuladır. Bu alanda edindiğimiz bilgiler, bize sadece geçmişi ve bugünü anlamamızı sağlamakla kalmaz, aynı zamanda geleceği şekillendirmemize, yaratıcı projeler geliştirmemize ve geleceğe yön vermemize de yardımcı olur.
Görsel Düşüncenin Matematiksel İfadesi
Analitik geometri, görsel dünyayı matematiksel bir dille ifade etmemizi sağlayarak, soyut kavramları somutlaştırmamıza olanak tanır. Şekillerin, desenlerin ve kompozisyonların altında yatan matematiksel prensipleri anlamamızı ve bu prensipleri kullanarak kendi tasarımlarımızı oluşturmamızı mümkün kılar.
Bir sanatçı, analitik geometriyi kullanarak tuvalindeki renklerin ve şekillerin dengesini kurabilir, perspektifi doğru bir şekilde uygulayabilir ve karmaşık desenler oluşturabilir. Bir mimar, binalarının tasarımında geometrik formları ve oranları kullanarak estetik ve işlevsel yapılar ortaya çıkarabilir. Bir grafik tasarımcı, logolar, web siteleri ve diğer görsel materyaller oluştururken analitik geometriden ilham alabilir.
Teknolojinin Yaratıcı Gücü
Analitik geometri, modern teknolojinin temel taşlarından biridir ve birçok farklı alanda yaratıcı uygulamalar için bir zemin hazırlar.
- Bilgisayar Grafikleri ve Oyun Geliştirme: Bilgisayar oyunlarındaki karakterlerin hareketleri, sanal dünyaların oluşturulması ve özel efektlerin yaratılması gibi birçok işlem, analitik geometri prensipleri kullanılarak gerçekleştirilir. Oyun geliştiriciler, analitik geometri sayesinde hayal ettikleri dünyaları gerçeğe dönüştürebilir ve oyunculara sürükleyici deneyimler sunabilir.
- Animasyon ve Görsel Efektler: Animasyon filmlerinde ve görsel efektlerde kullanılan karmaşık sahneler ve karakterler, analitik geometri yardımıyla modellenir ve canlandırılır. Animasyon sanatçıları, analitik geometri sayesinde hayal güçlerinin sınırlarını zorlayan yaratıcı eserler ortaya çıkarabilir.
- Mimari Tasarım ve Modelleme: Bilgisayar destekli tasarım (CAD) programları, mimarların ve mühendislerin karmaşık yapıları tasarlamasına ve modellemesine olanak tanır. Bu programlar, analitik geometri algoritmalarını kullanarak yapıların geometrisini, dayanıklılığını ve diğer özelliklerini analiz eder.
- Robotik ve Otomasyon: Robotların hareketlerini planlaması, çevrelerini algılaması ve nesneleri manipüle etmesi için analitik geometriye ihtiyacı vardır. Robotik mühendisleri, analitik geometri sayesinde robotların daha akıllı, daha verimli ve daha yetenekli olmasını sağlayabilir.
Yaratıcı Süreçte Analitik Geometri
Analitik geometri, sadece teknik bir araç değil, aynı zamanda yaratıcı sürecin kendisinin de bir parçası olabilir. Geometrik şekiller, desenler ve dönüşümler, sanatçılara, tasarımcılara ve diğer yaratıcılara ilham kaynağı olabilir.
- Geometrik Sanat: Birçok sanatçı, geometrik şekilleri ve desenleri kullanarak soyut sanat eserleri yaratır. Bu eserler, matematiksel düzenin ve estetiğin birleşimini temsil eder.
- Fraktal Sanat: Fraktallar, sonsuz karmaşıklığa sahip geometrik şekillerdir ve analitik geometri prensipleri kullanılarak oluşturulabilir. Fraktal sanat, matematiksel güzelliğin ve yaratıcılığın büyüleyici bir örneğidir.
- Tasarım ve Moda: Geometrik şekiller ve desenler, moda tasarımında, iç tasarımda ve diğer tasarım alanlarında sıkça kullanılır. Tasarımcılar, analitik geometriyi kullanarak estetik, işlevsel ve yenilikçi ürünler ortaya çıkarabilir.
Ayt Geometri hakkında daha fazla bilgi edinmek için bu makalemize göz atabilirsiniz.
Kendi Yaratıcılığımızın Keşfi
Analitik geometri, sadece dış dünyayı anlamamızı ve şekillendirmemizi sağlamakla kalmaz, aynı zamanda kendi iç dünyamızı keşfetmemize ve yaratıcılığımızı ifade etmemize de yardımcı olur. Geometrik düşünce, problem çözme becerilerimizi, analitik yeteneğimizi ve uzamsal algımızı geliştirir. Bu beceriler, sadece matematik ve bilim alanlarında değil, aynı zamanda sanat, tasarım, müzik ve diğer yaratıcı alanlarda da başarılı olmamızı sağlar.
Analitik geometri, bize yeni bir bakış açısı kazandırır, dünyayı farklı bir şekilde görmemizi sağlar ve yaratıcılığımızın sınırlarını zorlamamızı teşvik eder. Bu nedenle, analitik geometriyi öğrenmek ve kullanabilmek, sadece matematiksel bir bilgi değil, aynı zamanda kişisel ve profesyonel gelişimimiz için de önemli bir yatırımdır.
Bu yazıyı beğendiniz mi? Puanlayın!
Loading...
