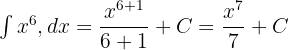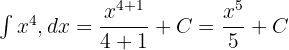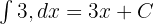Türev de integral de aslında değişim ile alakalıdır. Ancak izledikleri yol farklıdır. Türev, bir şeyin ne kadar hızlı değiştiğiyle alakadır. İntegral ise bir şeyin ne kadar değiştiğiyle alakalıdır. Yani asıl mesele niceliktir.
Bir doktorun hastasının tümörünün bir süre sonra ne kadar büyüyeceğini anlaması için integral gereklidir. Değişim hızının hesaplanması, her durumda bize kolaydık sağlar. Arabalardaki hız sabitleyici, arabanın ne kadar hızlanması veya yavaşlaması gerektiğini hesaplar. Kahve makineleri de güzel bir kahve için suyu tam olarak doğru sıcaklığa getirir. İşte bunlar için integral gerekir.
Yukarıda verdiğimiz örnekteki gibi bir tümörün ne kadar hızlı büyüdüğünü görmek için değişime bakarız. Tüm bunlar için aynı tekniği kullanıyoruz. Değişimin ne tür olduğu önemli değil çünkü hepsinin arka planında kullanılan matematik aynı!
Bir ay içinde kullandığınız toplam su miktarı, desteklediğiniz adayın seçimde yeniden seçilme şansı, bir borunun zamanla ne kadar bükülebileceği… Ne olursa olsun, bir şeyin ne kadar değiştiğini bilmek istediğimiz zaman integral kullanırız.
Hayattan Türev ve İntegral Örnekleri
Matematikçi olduğunuzu varsayalım. Bir araba fabrikasında çalışıyorsunuz ve göreviniz arabaları olabildiğince güvenli hâle getirmek. Bunu arabaları yakarak, ezerek, bir yerlere çarptırarak ölçebilirsiniz. Ama matematiği kullanarak çok fazla maddi hasar vermeden çözüme ulaşabilirsiniz.
Bildiğiniz gibi bir araba kazasında en büyük tehlike başımızdan hasar almamızdır. Çarpışmada başın ileri ya da geri hareketi hayati risklere yol açabilir. Aracın hızı, bu hareketin şiddeti konusunda çok etkilidir. İşte bu hızı ölçmek için diferansiyel denklemler kullanılabilir. Yani günümüzde arabaların daha güvenli hâle gelmesini de özünde matematiğe borçluyuz.
Diferansiyel denklemler yardımıyla herhangi bir çarpışma anında kafanın ne kadar hızlı hareket ettiğine bakabilirsiniz. Bu sayede de araca gerekli güvenlik donanımlarını bulabilirsiniz.
Bir matematikçi olarak kafanın hareketinin hızını hesaplamış oldunuz. Ama yine de kafanın hareket hızı ile çarpışmanın ne kadar tehlikeli olduğunu bilemezsiniz. İşte bu yüzden integrale ihtiyacınız olacak. Tehlikeyi tanımlayabilmek için çarpışma sırasında toplamda kafanın ne kadar hareket ettiğini bulmanız gerekir.
Diyelim ki kafanın bir saniyede öne arkaya iki kere hareket ettiğini buldunuz. Kaza 4 saniye sürdü. 2 kere 4, toplam 8 hareket ediyor diyemezsiniz. Bu hesap bu kadar basit olsa herkes bu gibi önerileri yapabilirdi.
Her ne kadar az bir süre zarfıymış gibi görünse de bir saniye bir kaza için büyük bir zaman dilimi.
Bu nedenle de saniye yerine çok daha küçük zaman birimlerini hesaba katıp, her zaman birimindeki hareketi belirleyip bunların toplamını alırsanız çözümümüz gerçeğe daha yakın olacaktır.
Araba fabrikalarındaki üreticiler, arabalarının güvenlik testlerinde bu hesaplamayı kullanıyorlar. Yani Instagram'da gördüğünüz kaza testleri aslında kazayı görselleştirmek için yapılıyor. Hesaplamalarda bu testler yeterli gelmiyor.
Türev ve İntegral Faydaları
Gördüğünüz gibi integral ve türev sürdüğünüz arabada, sabah kahvenizi demlediğiniz makinede, merkezi ısıtma sisteminizin termostatında, gittiğiniz doktorun raporlarında, gökdelenlerin ve köprülerin inşaasında… Her an her yerde!
Her yerde hesaplanması gereken değişimler vardır ve bu değişimleri hesaplamak, bu ikili olmadan neredeyse imkânsızdır.
Dünyada her şey sürekli değişir. Olan bitenleri incelemek için de aynı mantığı kullanırız. Ama türev ve integral öğrenme zorunluluğunuz aslında seçtiğiniz mesleğe göre değişir.
Günlük yaşamımızda türev ve integralin sağladığı avantajlardan faydalanıyor olsak da bu hesaplamaları yapmak zorunda kalmayız. Akademik açıdan bakacak olursak da matematik becerilerinizi kullanmanız gereken bir meslek seçmediğiniz sürece bu iki konu hakkında detaylı bilgi sahibi olmanıza gerek yok.
Hatta tahmin edebileceğiniz gibi öyle bir meslek seçseniz bile hesaplamaları artık bilgisayarlar yapıyor.
Ama bu konuları okulda öğreniyor olmak o kadar da boşa geçen bir zaman değil. Anlamak başta zor gelebilir ama işin özüne indiğinizde o kadar da zor olmadığını görebilirsiniz. Bu gibi örnekler verdiğimizde olaya sadece matematiksel açıdan bakmayı bırakıp günlük hayatınızla ilişkilendirmiş olduğunuzu umuyoruz. Mantığını kavramak da umarız işinizi kolaylaştırmıştır!
Etrafınızdaki dünyanın neyin nasıl olup bittiğini bilmek istiyorsanız işin özüne inmek çok önemlidir. Türev ve integral dünyayı tamamen değiştirdi. Bilgisayarları, akıllı telefonları, kablosuz kulaklıkları, otomatik kahve makinelerini, uçakları ve diğer birçok modern makineyi mümkün kıldılar. Onlar olmasa şimdi çok farklı bir dünyada yaşıyor olurduk.
Basit Türev ve İntegral Soruları
Örnek 1
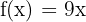fonksiyonunun türevini bulun.
Çözüm 1
Bu işlevi şu şekilde yazabiliriz:
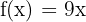
Değişkenin türevi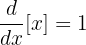 
olduğundan, 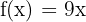fonksiyonunun türevi de şöyle olur:
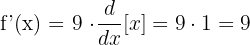
Matematiksel olarak şu şekilde gösterilebilir:
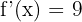
Örnek 2
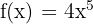fonksiyonunun türevini bulun.
Çözüm 2
Yukarıdaki fonksiyonun türevini alırken iki temel türev kuralını kullanabiliriz. Birincisi, fonksiyon sabit bir 4 ile çarpıldığı için, fonksiyonu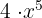 
olarak yazabiliriz ve şöyle yapabiliriz:
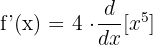
Şimdi 
’ün türevini bulmamız gerekiyor çünkü bir sabiti bir fonksiyonla çarptığımızda fonksiyonun türevini buluyoruz ve sabiti onunla çarpıyoruz.
’ün türevini bulmak için kuvvet kuralını burada uygulayalım:
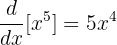
Yukarıdaki türev fonksiyonunu basitleştirince şu sonuca ulaşırız:
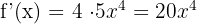
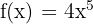fonksiyonunun türevi:
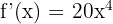
Soru 3
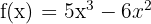fonksiyonunun türevini bulun.
Çözüm 3
Birinci terimin türevi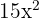 
. Benzer şekilde, ikinci terimin türevi de 
.
Tüm fonksiyonun türevini şu şekilde yazmak için türev farkı kuralını kullanacağız:
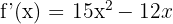
Çıkarmanın aritmetik işareti, türev farkı kuralına göre aynı kalacaktır.
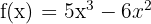fonksiyonunun türevi:
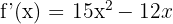
Örnek 4
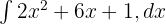kaçtır?
Çözüm 4
İlk adımda, toplama/çıkarma veya sabitlerle çarpma gibi belirli integral kurallarını kullanarak integralleri parçalayacağız.
Bu kuralları kullanarak yukarıdaki işlevi şu şekilde yeniden yazabiliriz:
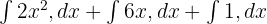
Bir sonraki adımda, aşağıda gösterildiği gibi integral işaretlerinden önceki sabitleri kaydıracağız:
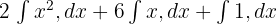
İntegrallerin kuvvet kuralını hatırlayın:
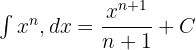
Bu kuralı, yukarıdaki polinomun sabit teriminin integralini bulmak için kuvvetlerin ve integral sabit kuralının integrallerini hesaplamak için kullanacağız:
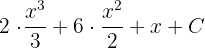
Son adımda cevabı şu şekilde en basitleştirilmiş hâliyle yazabiliriz:
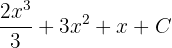
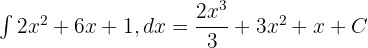
Soru 5
Aşağıdaki üstel fonksiyonun integralini hesaplayın:
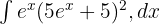
Çözüm 5
Aşağıdaki işlevi elde etmek için yukarıdaki üstel işlevi genişletin:
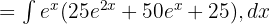
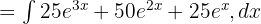
Şimdi, yukarıdaki işlevi şu şekilde yazmak için integralde toplama kuralını kullanacağız:
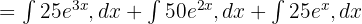
Her terimin integralini ayrı ayrı şu şekilde hesaplayacağız:
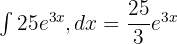
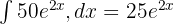
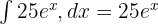
Yukarıdaki integralleri kullanarak cevabı şu şekilde yazabiliriz:
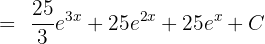
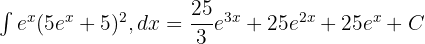
Soru 6
Aşağıdaki üstel fonksiyonun integralini bulun:
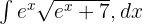
Çözüm 6
Bu soruyu yerine koyma yöntemini kullanarak çözeceğiz.
- Yerine Koyma:
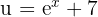diyelim.
Bu da şu anlama gelir: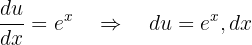
- İntegrali Yeniden Yazma:
Aşağıdakileri elde etmek için bu değerleri yukarıdaki denklemde değiştirin: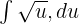
- İntegrali Hesaplama:
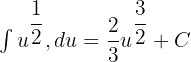
- Basitleştirme ve Yerine Koyma: 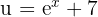olduğundan, son cevabı bulmak için yukarıdaki denklemi tekrar yerine koyun: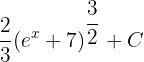
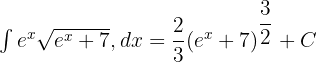
Soru 7
Aşağıdaki fonksiyonun integralini bulun.
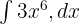
Çözüm 7
Yukarıdaki fonksiyon güç veya üs içerdiğinden, integrali hesaplamak için aşağıdaki formülü kullanacağız:
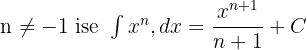
Bu soruda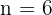 
. Şimdi bu değeri yukarıdaki formüle koyacağız:
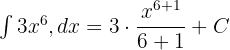
Yukarıdaki denklemi basitleştirmek bize aşağıdaki cevabı verir:
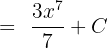
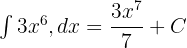
Soru 8
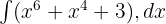
Çözüm 8
Yukarıdaki fonksiyon hem üslü hem de sabit değişkenler içerdiğinden, integrali hesaplamak için aşağıdaki formülleri kullanacağız:
- Üs için:
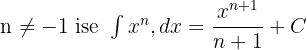
- Sabit için:
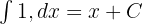
Ancak bu formülleri uygulamadan önce, integralde toplama kuralını kullanarak soruyu şu şekilde yeniden yazacağız:
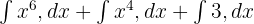
Bunun gibi üç terimin ayrı ayrı integralini bulacağız:
Şimdi de tüm fonksiyonun integralini yazmak için bu cevapları tekrar birleştireceğiz:
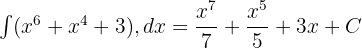
Özel Derslerle Türev ve İntegrali Daha İyi Anlama
Özel dersler, çalışma ve öğrenme becerilerinizi geliştirmenize yardımcı olabilir. Bu da hayatınız boyunca başarıya ulaşmanızı sağlamaya yardımcı olur. Özel derslerin birçok avantajı vardır:
- Bireysel ve benzersiz öğrenme deneyimi: Öğretmeniniz dersleri size ve ihtiyaçlarınıza göre uyarlayabilir.
- Öğretmenin dikkati sizde olur: Öğretmeniniz bireysel öğrenme stilinizi tanır ve öğretim yöntemlerini buna göre uyarlayabilir.
- Akademik performansı artırır: Özel derslerde öğretmeniniz sizi testlere ve sınavlara hazırlarken güçlü yanlarınızı ortaya çıkarır ve zayıf olduğunuz noktalarda size yardımcı olur.
- Tek başınıza nasıl ders çalışacağınızı daha iyi anlarsınız: Öğretmeninizden farklı çalışma teknikleri öğrenirsiniz. Kendisinden size bir çalışma programı hazırlamasını isteyebilirsiniz.
- Kendinize olan güveniniz artar: Öğretmeniniz başarılı olmak için ihtiyaç duyduğunuz kaynakları ve becerileri sağlayarak öz güveninizi arttırabilir.
- Pozitif çalışma alanı: Özel derslerde öğrenmeye daha iyi odaklanırsınız. Etrafınızda dikkat dağıtan kimse olmaz.
- Öğrenme engellerinizin üstesinden gelmenize yardımcı olur: Öğrenmenin hangi alanında sorun yaşıyorsanız öğretmeniniz onu özellikle hedef alacaktır.
- Tam ihtiyacınız olan eğitimi almanızı sağlar: Böylece vaktinizi en iyi şekilde değerlendirmiş olursunuz. Emin adımlar atarak hızla ilerlersiniz!
Superprof'taki özel ders öğretmenlerinden isterseniz sadece türev ve integral konusunda yardım alabilirsiniz. Ayrıca Ankara matematik özel ders ve diğer lokasyonlardaki matematik özel ders seçeneklerine göz atıp sizin için en uygununu seçebilirsiniz. Derslere istediğiniz zaman başlayıp istediğiniz zaman bırakabilirsiniz. Sınava hazırlanıyorsanız bu süreç boyunca yanınızda rehberlik edecek biri olması için ders almaya devam edebilirsiniz. Derslerinizin gününü ve saatini programınıza göre uydurabilirsiniz. İpler sizin elinizde!
Bu yazıyı beğendiniz mi? Puanlayın!
Loading...
