Maya Uygarlığı denildiğinde akla ilk olarak gizemli takvimleri ve astronomik hesaplamaları gelir. Maya sayı sistemi, bu eski medeniyetin bilim ve inanç dünyasında merkezi bir rol oynamıştır. Maya’lar, Maya rakamları ile yalnızca üç basit sembol kullanarak çok büyük sayıları ifade edebiliyordu. Onların geliştirdiği bu sistem, takvimlerinden mimari planlarına kadar pek çok alanda kullanıldı. Peki Maya sayıları nasıl çalışıyordu ve neden bu kadar özeldir?
Bu yazımızda Maya matematiğinin temellerini, Maya sembolleri ve anlamları dahil olmak üzere inceleyecek; takvimleriyle ilişkisini, günümüze kalan mirasını keşfedeceğiz.
Kısaca Maya Uygarlığı ve Matematiğe Bakışı
Orta Amerika’nın antik halklarından olan Maya’lar, yaklaşık MÖ 2000’lerden itibaren gelişmeye başlayan ve MS 16. yüzyıla dek varlığını sürdüren bir uygarlıktı. Kendi dilleri ve hiyeroglif yazı sistemleri vardı. Mimaride piramit tapınaklar, astronomide ileri gözlemler ve karmaşık takvim sistemleri geliştirdiler.
Maya’ların entelektüel ve sanatsal seviyesi, döneminin Yeni Dünya toplumları arasında benzersizdi. Bu başarıların ardında, güçlü bir matematik altyapısı bulunuyordu. Nitekim birçok erken medeniyette olduğu gibi, Maya’lar da takvim oluşturmak ve gök olaylarını hesaplamak için gelişmiş bir sayı sistemi ve matematiksel bilgi geliştirmişlerdi.
Maya’lar sayılarını taş anıtlar ve tapınak duvarlarına oyarak kayıt altına bıraktılar. Ne yazık ki, kağıt benzeri malzemeye yazdıkları eserlerin (kodekslerin) büyük kısmı İspanyollar tarafından yok edildi. Günümüzde Maya’lara ait yalnızca birkaç elyazması kitap (yalnızca dört tane olduğu biliniyor) hayatta kalabilmiştir. Bu yüzden Maya matematiğiyle ilgili bilgilerimizin çoğu, kazılarla ortaya çıkarılan taş stellerdeki Maya rakamları ve yazıtlardan geliyor. Bu ipuçları, Maya toplumunun matematiğe ve özellikle zaman hesaplarına verdiği önemi gösteriyor.
Mayalara dair etkileyici ve bilgi dolu bir video önerisi;
Maya Sayı Sistemi Nasıl Çalışır?
Maya’lar, modern dünyada kullandığımız onluk sistemden farklı olarak yirmilik tabana dayalı (vigesimal) bir sayı sistemi geliştirmişlerdi. Yani basamak değerleri 10’un değil 20’nin katları şeklinde ilerliyordu. Muhtemelen bunun nedeni, sadece el parmaklarını değil el ve ayak parmaklarının toplamını (20 parmak) saymada temel almalarıydı. Sonuç olarak Maya sayı sisteminde 1’den 19’a kadar olan değerler tek bir basamakta gösterilebiliyordu; 20 sayısına gelindiğinde yeni bir basamak ekleniyordu. Bu yapı, tıpkı bizim onluk sistemimizde 9’dan sonra basamak atlayıp 10’a geçmemize benzer şekilde, 19’dan sonra bir üst basamağa geçilmesiyle çalışıyordu.
Mayaların geliştirdiği sistem, özellikle 60 tabanlı sayı sistemi gibi çok tabanlı yapılara ilham verecek kadar gelişmişti.
Maya sembolleri ve anlamları oldukça basitti. Bu sistemde sayılar sadece üç sembolle ifade ediliyordu.
Bir noktacık “1” değerini, yatay bir çizgi “5” değerini gösteriyordu. Üçüncü sembol ise bir kabuk veya deniz salyangozu kabuğu şekli olup “0” (sıfır) değerini temsil ediyordu. Maya’lar sıfırı basamakları boş bırakmak yerine özel bir sembolle göstererek diğer birçok antik medeniyetten ayrılıyordu. Mayaların 20 tabanlı sayı sisteminde toplam 19 farklı sayı sembolle temsil edilebiliyordu (0 dahil edilirse 20 farklı işaret).
Örneğin 1’den 19’a kadar olan Maya rakamları, nokta ve çizginin çeşitli kombinasyonlarıyla şu şekilde yazılıyordu.
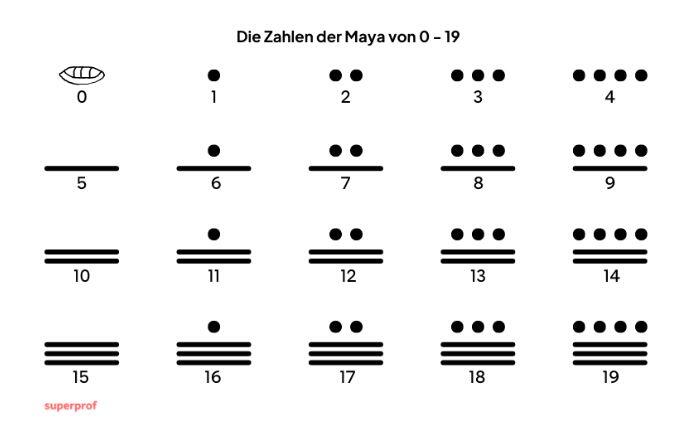
Maya sayıları 0’dan 19’a kadar kabuk (0), nokta (1) ve çizgi (5) sembolleriyle gösteriliyordu. Örneğin 14 sayısı, Maya sisteminde iki yatay çizgi (10 değeri) ve dört nokta (4 değeri) kombinasyonuyla aynı seviyede yazılırdı. Bu basit semboller sayesinde Maya’lar, 19’a kadar olan tüm sayıları kolaylıkla ifade edebiliyordu.
Sayıların anlamını kavramak isteyenler için, Antik Mısır’daki sayı stilleri oldukça etkileyici bir örnektir.
Maya Rakamları ve Basamak Değerleri
Maya sayıları, basamaklı bir sistem içinde kullanılıyordu. Yani bir sayının birler, yirmiler, dört yüzler gibi basamak değerleri vardı. Biz bugün onluk sistemde çok basamaklı sayıları yatay olarak yan yana yazarız ve en sağdaki basamak 10^0 (birler), onun solu 10^1 (onlar), sonra 10^2 (yüzler) şeklinde değerlenir. Maya’lar ise benzer mantığı dikey olarak uyguluyordu: Maya rakamları yan yana değil, alt alta yazılırdı. En alttaki sembol, sayının birler basamağı (20^0) idi. Onun hemen üstüne yazılan sembol, sayının yirmiler basamağı (20^1) değerini temsil ederdi. Bir basamak yukarı çıkıldığında, değeri bir alt basamağın 20 katı olacak şekilde artardı.
Maya medeniyeti, “0” rakamını sembol olarak kullanan en eski uygarlıklardan biridir. Hatta bazı kaynaklar, Maya’ların sıfırı Hindistan’daki kullanımından yaklaşık 1000 yıl önce keşfedip kullandığını belirtir
Bu sistemi anlamak için bir örnek verelim.
- Modern ondalık sistemde 235 sayısı, basamak değeriyle 2×10^2 + 3×10^1 + 5×10^0 şeklinde çözümlenir.
- Benzer şekilde bir Maya sayısı için, alttaki sembol 20^0 ile, üstündeki semboller sırasıyla 20^1, 20^2, 20^3 ... ile çarpılır.
Örneğin Maya rakamlarıyla yazılmış iki basamaklı bir sayı düşünelim.
Altta 13, üstünde 1 sembolü olsun. Alttaki 13, birler basamağında “13” değerini, üstteki 1 ise yirmiler basamağında “1×20” yani 20 değerini temsil eder. Bu iki değer toplanarak 33 sayısı elde edilir. Gerçekte bu sayı, Maya yazısıyla alt alta dizilmiş bir nokta (üstte) ve onun altında iki çizgi üzerindeki üç noktadan oluşur. Yani 1×20 + 13 = 33 sonucunu verir. Benzer şekilde, Maya sisteminde üç basamaklı bir sayı yazmak, 20^2 (400’ler) basamağını eklemek anlamına gelir. Bu yapı sayesinde Maya’lar, teorik olarak çok yüksek değerlere kadar sayıları yazabiliyordu.
Yüzlerce yıl sonra Roma'da, Romen rakamları gibi daha sınırlı sistemlerin neden tercih edildiğini merak etmemek elde değil.
Örneğin üç basamaklı en büyük Maya sayısı 19.19.19 biçiminde yazılarak 19×20^2 + 19×20^1 + 19 = 7999 sayısını ifade ediyordu. Dört basamak ile 20^3 (8000’ler) devreye giriyor, beş basamakla 20^4 (160.000’ler) ve altı basamakla 20^5 (3.200.000'ler) gibi astronomik büyüklükler bile temsil edilebiliyordu. Bu, o dönemde başka hiçbir yazılı sayı sisteminin kolay kolay başaramadığı bir şeydi.
Toplama ve çıkarma gibi işlemler Maya sisteminde oldukça basit şekilde yapılabiliyordu. Çünkü sembolleri anlamak kolaydı.
Örneğin iki Maya sayısını toplamak için, alt alta yazılmış semboller düzeyinde noktaları ve çizgileri bir araya getirmek yeterliydi – her beş nokta bir çizgiye dönüşür, her dört çizgi bir üst basamağa taşınırdı. Bu yönüyle Maya sayı sistemi, şaşırtıcı derecede pratik ve esnekti. Çarpma ve bölme gibi daha karmaşık işlemler içinse arkeologlar bazı tablo şeklinde dizilmiş sayılar bulmuştur; bu tablolar muhtemelen pratik birer hesaplama aracı olarak kullanılıyordu. Yani Maya’lar matematiksel işlemleri desteklemek için erken dönem “hesap cetvelleri” bile geliştirmişti.
Tarihte hiçbir toplum, Maya’lar kadar zamana böylesine derin bir ilgi göstermemiştir; hiçbir kültür de bu denli sıradışı bir konuyu kucaklayan bir felsefe geliştirmemiştir.”
Eric J. Thompson (Maya araştırmacısı)
Takvimlerde Maya Sayıları ve 20 Tabanı
Maya sayı sisteminin en çarpıcı uygulaması, takvimlerinde görülür. Maya’lar en az üç farklı takvim kullanmıştı: Bunlardan biri 365 günlük Haab takvimi (güneş yılına dayalı), biri 260 günlük Tzolkin takvimi (ritüel yıl), diğeri de çok uzun periyotları saymaya yarayan Uzun Sayım takvimiydi. Bu takvimlerin hepsinde Maya sayı sistemi kullanılmaktaydı. Özellikle “Uzun Sayım” (Long Count) takvimi, başlangıç olarak MÖ 3114 tarihini alır ve her günü o başlangıçtan itibaren geçen gün sayısıyla tanımlardı. Uzun Sayım takviminde tarihleri kaydetmek için ardışık 5 basamaklı bir sayı sistemi kullanılıyordu. Bu basamaklar, küçükten büyüğe doğru şöyleydi.
- 1 Kin = 1 gün (bir günlük süre)
- 20 Kin = 1 Uinal = 20 günlük “ay” (ay adı verilen dönem)
- 18 Uinal = 1 Tun = 360 gün (yaklaşık 1 “yıl”)
- 20 Tun = 1 Katun = 7.200 gün (yaklaşık 20 yıl)
- 20 Katun = 1 Baktun = 144.000 gün (yaklaşık 394 yıl)
yapar. Maya Uzun Sayım takviminde 13 Baktun’luk döngüler büyük önem taşır. Örneğin 13 Baktun ≈ 5125 yıl yapar ve 2012’de böyle bir döngü tamamlanmıştır
Görüldüğü gibi Maya’lar, takvim hesaplarında ikinci basamak olarak 18 kullanarak 360 günlük bir yılı esas almışlardı. Haab takvimindeki 18×20 = 360 günlük dönem, artan 5 artık gün (Wayeb ayı) ile birlikte 365 günlük Güneş yılını oluşturuyordu. Bu sayede 20 tabanlı sistemlerini takvim döngülerine uyarlayabilmişlerdi. Maya takvimi hayli karmaşık olsa da, altında yatan matematiksel prensip basamaklı Maya sayı sistemiydi.
Maya’lar, Haab (365 günlük yıl) ve Tzolkin (260 günlük yıl) takvimlerini bir arada kullanarak daha uzun döngüler de tanımladılar. 52 Haab yılı (yani 52×365 gün) geçtikten sonra Haab ve Tzolkin takvimleri tekrar aynı başlangıç noktasına gelirdi; bu süreye Takvim Dairesi (Calendar Round) denirdi. Ancak daha da uzun süreleri kaydetmek için Uzun Sayım takvimi devreye giriyordu. Uzun Sayım’da her gün beşli basamak sistemiyle (baktun.katun.tun.uinal.kin) numaralandırıldı. Örneğin, 13.0.0.0.0 ifadesi, Maya takviminde 13 baktun geçmiş, daha küçük birimlerin ise sıfırlandığı bir tarihti. Modern takvime göre bu tarih 21 Aralık 2012’ye karşılık gelir.
Bütün bu sistemlerin ortak noktaları, antik dünyanın sayı sistemleri üzerine düşünmeyi fazlasıyla hak ediyor.
Bu tarih, Maya takviminde büyük bir döngünün tamamlanması olduğu için zamanında çok sansasyon yaratmıştı. Hatta bazı çevrelerce “Maya takviminin sonu” olarak yorumlanıp kıyamet kehanetlerine bile konu edildi. Oysa gerçekte Maya takvimi 13. baktun sonunda bitmiyordu – Maya’lar gerektiğinde baktunların ötesinde daha büyük zaman birimlerini de tanımlamışlardı. Nitekim bilim insanlarının tespitine göre Maya’lar, milyonlarca yılı ölçebilecek daha büyük döngü birimlerini bile düşünüp adlandırmıştı. Dolayısıyla 2012’de sadece bir döngü tamamlanmış, takvim çarkı tekrar başa sarmıştı; Maya’lar yeni bir çağın başlayacağına inanmış olabilirlerdi ama dünyanın sonunun geleceğine dair bir ifade yoktu.
Bu yazıyı beğendiniz mi? Puanlayın!
Loading...
