Aritmetik, öğrencilerin ilkokuldan itibaren öğrendiği ve her sınıf seviyesinde önemli olan matematiğin temel becerilerinden biridir. Bu yöntem sayesinde toplama, çıkarma, çarpma ve bölme gibi matematiksel işlemler adım adım ve yazılı olarak çözülebilir.
Aritmetik yalnızca teknik bir işlem değil aynı zamanda mantıksal düşünmeyi ve problem çözme becerilerini geliştirir. Bu yazıda; toplama, çıkarma, çarpma ve bölme işlemlerinin yazılı yöntemleri detaylı bir şekilde ele alınırken, bu işlemleri daha kolay ve anlaşılır hale getiren pratik ipuçları ve püf noktaları da paylaşacağız.
Elde ile toplama, onluk bozarak çıkarma, büyük sayılarla çarpma ya da kalanlı bölme gibi dört işlemin en zorlayıcı bölümlerini de öğrenerek her birini rahatça uygulayabileceksiniz. Toplama çıkarma işlemleriyle başlamadan önce dört işlem terimlerine gelin göz atalım:
| İşlem | Terimler | Sonuç Adı |
|---|---|---|
| Toplama | Toplanan + Toplanan | Toplam |
| Çıkarma | Eksilen − Çıkan | Fark |
| Çarpma | Çarpan × Çarpılan | Çarpım |
| Bölme | Bölünen ÷ Bölen | Bölüm (+ Kalan) |

Toplama İşlemi
Alt alta toplama, matematikte herkesin bilmesi gereken temel yöntemlerden biridir. Mantık çok basit: İki ya da daha fazla sayıyı alt alta yazar, sonra da sağdan sola doğru (yani birler basamağından başlayarak) toplarsın. Her basamaktaki sonucu, çizginin altına aynı basamağın hizasına yazarsın. Bu sayede özellikle büyük sayıları bile adım adım, hata yapmadan toplamak çok daha kolay olur.
Eldeli (Taşımalı) Toplama
Peki çizginin altına yazman gereken sonuç iki basamaklı olursa ne olacak? İşte burada “elde” (taşıma) devreye girer.
Eğer bir basamaktaki toplam 9’dan büyükse, sonucun birler hanesini aşağı yazarsın; onlar hanesini ise bir sonraki basamağa (soldaki basamağa) elde olarak eklersin.
Örnek: 467 + 589
- Önce birler basamağı: 7 + 9 = 16
- 6’yı birlerin altına yaz, 1’i elde olarak onlar basamağına taşı.
- Sonra onlar basamağı: 6 + 8 + 1 (elde) = 15
- 5’i onlar basamağına yaz, 1’i yüzler basamağına taşı.
- Böyle böyle devam ederek işlem tamamlanır.
Bu yöntemle, kaç basamaklı olursa olsun sayıları düzenli ve güvenli bir şekilde toplayabilirsin.
Ondalıklı Sayıların Alt Alta Toplanması
Ondalıklı sayılarla toplama yaparken en önemli kural, virgülleri tam alt alta gelecek şekilde hizalamaktır. Örneğin 47,5 + 3,75 işlemini ele alalım. Sayıları yazarken ondalık kısımların aynı sütunda olmasına dikkat ederiz. Daha sonra toplama işlemini her zamanki gibi yapar, sonuçtaki virgülü de yine virgüllerin tam altına yazarız.
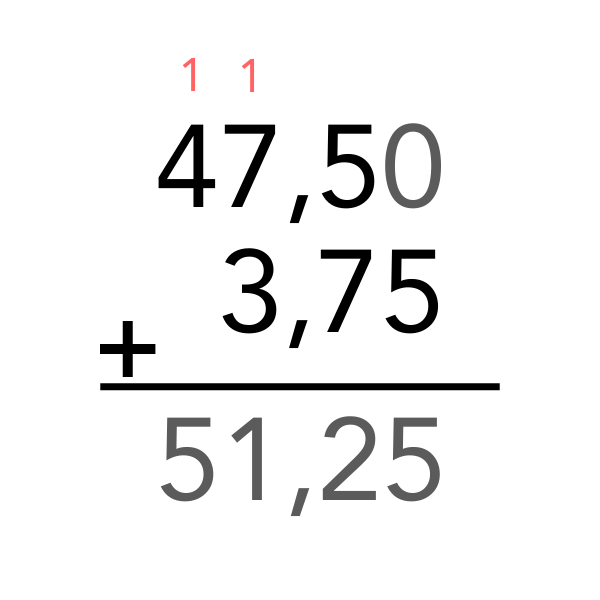
Adım adım örnek: 47,5 + 3,75
- Sağdan sola doğru başlarız:
0 + 5 = 5 - 7 + 5 = 12 → 2 yazılır, 1 elde edilir
- Ardından virgül gelir
- 7 + 3 + 1 (elde) = 11 → 1 yazılır, 1 elde edilir
- 4 + 1 = 5
Sonuç olarak: 47,5 + 3,75 = 51,25
Biraz pratik ve birkaç problem çözdükten sonra ister ondalıklı sayılarla, ister eldeli ya da büyük sayılarla olsun, toplama işlemlerinin sana çok daha kolay geldiğini fark edeceksin.
Dört işlem yaparken sayıları alt alta, basamaklarına göre hizalayın. Virgüllü işlemlerde ise virgüller mutlaka alt alta gelmeli; böylece hata ihtimali ciddi şekilde azalır.
Çıkarma İşlemi
Çıkarma, sayıları alt alta yazarak basamak basamak çıkarma işlemidir ve matematiğin temel becerilerinden biridir. İlkokulda öğretilir ve daha ileri matematik konularını anlayabilmek için oldukça önemlidir.
Toplamada olduğu gibi burada da sağdan sola doğru ilerleriz ve alttaki sayıyı, üstteki sayıdan çıkarırız.
Örneğin 1785 − 562 işleminde adımlar şöyledir:
- 5 − 2 = 3
- 8 − 6 = 2
- 7 − 5 = 2
- 1 − 0 = 1
Sonuç:
1785 − 562 = 1223
Eldeli (Onluk Bozarak) Alt Alta Çıkarma
Bazı durumlarda, çıkarılacak sayının bir basamaktaki rakamı, üstteki sayıdan daha büyük olabilir. Bu durumda elde alma ya da diğer adıyla onluk bozma yöntemi kullanılır.
Bu yöntemde, üstteki sayının bir üst basamağından 1 onluk ödünç alınır. Alınan bu onluk, alt basamağa eklenir; ödünç alınan basamak ise 1 azaltılır.
Adım Adım Örnek: 705 − 387
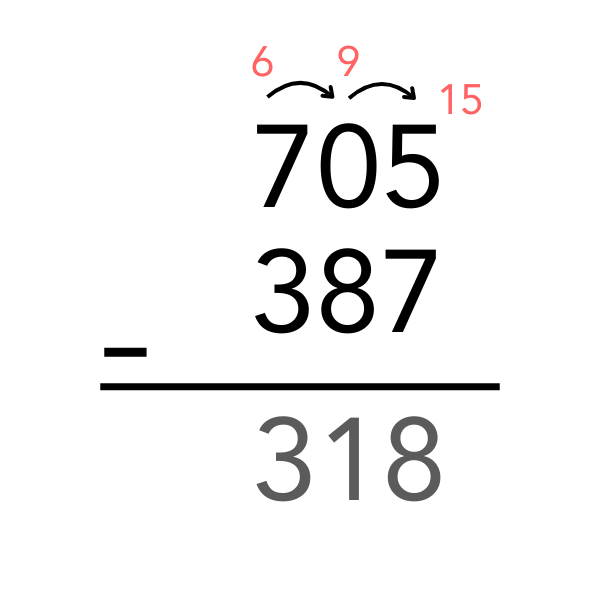
Birler basamağı:
5, 7’den küçük olduğu için onlar basamağından 1 onluk ödünç alınır.
Ancak onlar basamağında 0 olduğu için önce yüzler basamağından bir onluk alınır. Böylece yüzler basamağı 6 olur, onlar basamağı 9’a dönüşür. Birler basamağına 10 eklenir ve 5 → 15 olur.
Birler basamağı:
15 − 7 = 8
Onlar basamağı:
9 − 8 = 1
Yüzler basamağı:
6 − 3 = 3
Sonuç: 705 − 387 = 318
Biraz pratik yaptıktan sonra, ister basit ister eldeli olsun, yazılı çıkarma işlemlerinin çok daha anlaşılır ve kolay hale geldiğini göreceksin.
Ondalıklı Sayılarla (Virgüllü) Çıkarma İşlemi
Ondalıklı (virgüllü) sayılarla çıkarma yaparken, tıpkı toplamada olduğu gibi, virgüllerin tam alt alta gelecek şekilde hizalanması çok önemlidir. Bu sayede ondalık basamaklar doğru konumlanır ve işlem hatasız yapılır.
Örnek:
15,75 − 3,2 işlemi, önce basamakları eşitleyerek;
15,75 − 3,20
şeklinde yazılır. Ardından çıkarma işlemine geçilir. Çıkarmaya sağdan sola doğru başlanır ve sonuçtaki virgül, diğer virgüllerin tam altına yazılır.
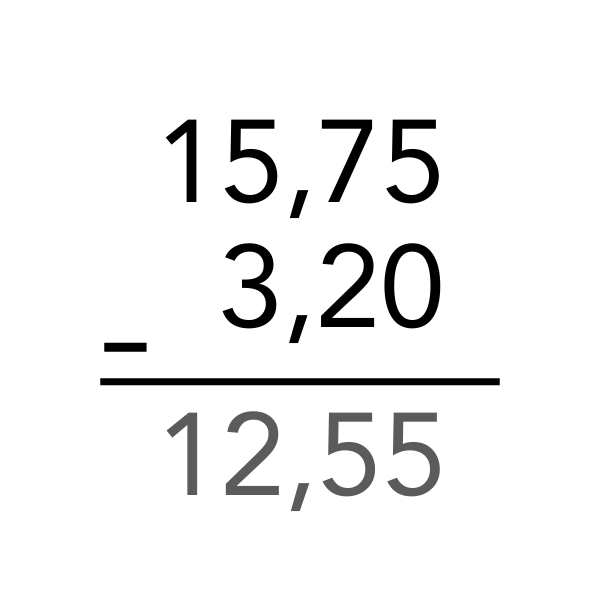
Tamamlama Yöntemi
Çıkarma yöntemi, en sık kullanılan klasik yöntemdir. Bu yöntemde alt sıradaki rakam, üst sıradaki karşılık gelen rakamdan çıkarılır. Eğer üstteki rakam daha küçükse, onluk bozma (elde alma) yapılır.
Tamamlama yöntemi ise farklı bir bakış açısı sunar. Bu yöntemde, alttaki sayıya hangi değerin eklenmesi gerektiği hesaplanarak üstteki sayıya ulaşılır. Özellikle daha karmaşık veya büyük sayılarla yapılan işlemlerde, bu yöntem süreci kolaylaştırabilir.
Örneğin: 500 − 378 = ?
Bu işlemi klasik çıkarma yerine tamamlama yöntemiyle düşünelim. Amacımız şunu bulmak: 378’e hangi sayıyı eklersek 500’e ulaşırız?
378 → 380 (+2)
380 → 400 (+20)
400 → 500 (+100)
Şimdi eklenenleri toplayalım:
- 2 + 20 + 100 = 122
Sonuç:
500 − 378 = 122
Her iki yöntemi de öğrendiğinde, ondalıklı sayılarla yapılan çıkarma işlemlerini daha hızlı ve güvenli bir şekilde çözebilirsin.
Bölme İşlemi
Bölme, bir sayıyı başka bir sayıya bölerek bölümü ve gerekiyorsa kalanı bulmamızı sağlayan temel bir matematik becerisidir. Bölme işlemi genel olarak üç temel adımda yapılır.
Bölmenin Temel Adımları
- Bölünenin soldan ilk rakamını, bölen ile böl.
- Bulduğun bölüm basamağını, bölenle çarp ve sonucu eksi işaretiyle bölünenin altına yaz.
- Çıkarma işlemi yap ve bir sonraki rakamı aşağı indirerek işleme devam et.
Adım Adım Örnek: 853 ÷ 4
1. adım:
Soldan başlarız: 8 ÷ 4 = 2
→ 2, bölümün ilk rakamıdır.
2. adım: 2 × 4 = 8
→ 8’i, 8’in altına eksi işaretiyle yazarız.
3. adım: 8 − 8 = 0
4. adım: Bölünenin bir sonraki rakamını aşağı indiririz. 5’i, elde ettiğimiz 0’ın yanına yazarız

Tekrar 1. adım:
5 ÷ 4 = 1 (çünkü 4, 5’in içinde 1 kez vardır)
→ 1, bölümde 2’nin yanına yazılır.
2. adım: 1 × 4 = 4
→ 4’ü, 5’in altına yazarız.
3. adım: 5 − 4 = 1
4. adım: Bölünenin son rakamı olan 3’ü aşağı indiririz: 1’in yanına 3 gelir → 13
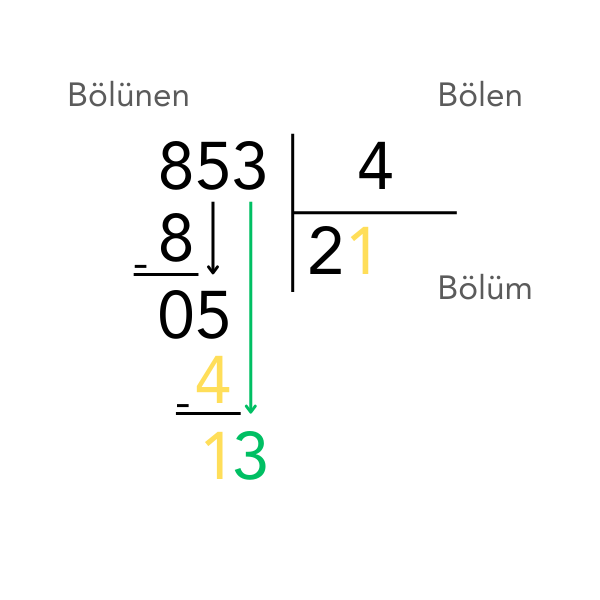
Aynı işlemler tekrar uygulanır.
13 ÷ 4 = 3
→ 3, bölümün son rakamıdır.
3 × 4 = 12
12’yi, 13’ün altına yazarız.
13 − 12 = 1
Sonuç: 853 ÷ 4 = 213 kalan 1
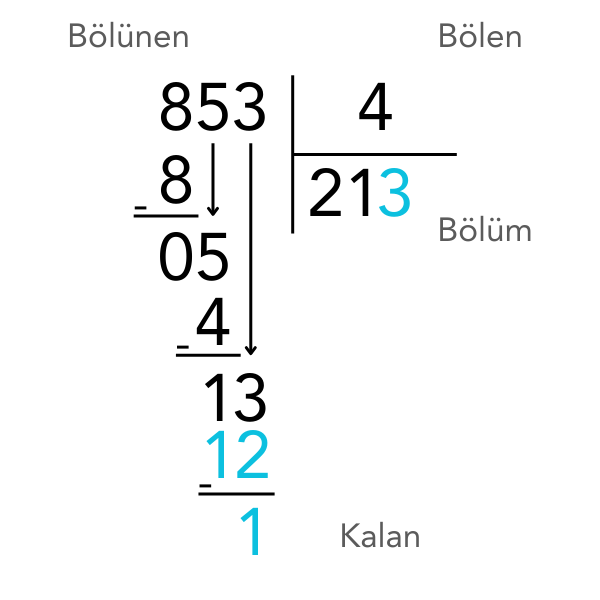
Yazılı bölmede mantığı anladığında, işlem uzun görünse bile aslında aynı adımların tekrarından ibaret olduğunu fark edeceksin. Biraz pratikle yazılı bölme de diğer işlemler kadar kolay hale gelir.
Ondalıklı Sayıların Bölünmesi
Ondalıklı sayılarla bölme yaparken, bölümdeki virgül, bölünen sayıdaki virgülün tam hizasına gelecek şekilde yazılır. Bölünen sayı tamamen bölündükten sonra gerekiyorsa, işlemi sürdürebilmek için sona sıfırlar eklenebilir. Bu, sonucun değerini değiştirmez, sadece bölmeyi tamamlamayı sağlar.
Örnek:
12,4 ÷ 2 = 6,2
Büyük Sayılarla Bölme
Büyük sayılarla yapılan bölme işlemi, mantık olarak küçük sayılarla yapılan bölmeden farklı değildir. Ancak daha fazla adım ve dikkat gerektirir. Bu tür işlemlerde, bölünen sayıyı daha küçük ve yönetilebilir parçalara ayırarak ilerlemek faydalıdır.
Böleni, bölünenin en büyük basamağından başlayarak adım adım çıkarır ve her aşamada aynı bölme kurallarını uygularsın. Sabırlı ve düzenli ilerlediğinde, büyük sayılarla yapılan bölmenin de aslında karmaşık olmadığını göreceksin.
Çarpma İşlemi
Çarpma işlemi, büyük sayıları adım adım çarpmayı sağlayan temel matematik yöntemlerinden biridir. Özellikle ölçü birimleri arasında dönüşüm yaparken ya da çok basamaklı sayılarla işlem yaparken büyük kolaylık sağlar.
Çarpma Nasıl Yapılır?
Çarpma işlemi için önce işlemi düzgün bir şekilde yazarsın.
- Üstteki sayı çarpılan
- Alttaki sayı çarpan olarak alınır.
Önce alttaki sayının sağdan ilk rakamı ile üstteki sayı çarpılır. Elde edilen ara sonuç (kısmi çarpım) çizginin altına yazılır. Daha sonra alttaki sayının diğer rakamlarıyla aynı işlem yapılır. Her yeni ara sonuç, bir öncekinin bir basamak soluna kaydırılarak yazılır. Son aşamada ise tüm ara sonuçlar toplanarak nihai sonuç elde edilir.
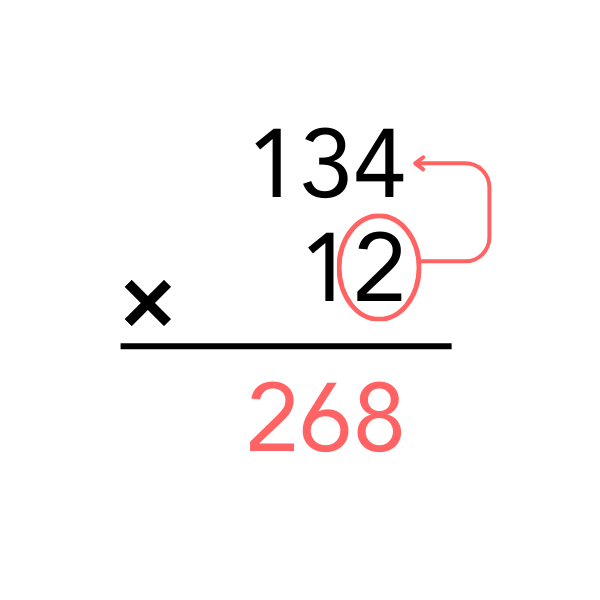
Adım Adım Örnek: 134 × 12
- Öncelikle çarpılan ile çarpanın birler basamağındaki sayı çarpılır:
- 134 x 2 = 268
- Bu sonucu çizginin altına yazarız.
- Ardından çarpılan ile çarapanın onlar basamağındaki sayı çarpılır:
- 134 × 1 = 134
- Bu sonucu, bir basamak sola kaydırarak 268’in altına yazarız.
- Sola kaydırmamızın sebebi çarpılanı 1 ile değil, onlar basmağında olduğu için 10 ile çarpmamız, dolayısıyla sonda hayali bir 0 olacaktır.
- Son olarak iki ara sonucu toplarız:
1340 + 268 = 1608
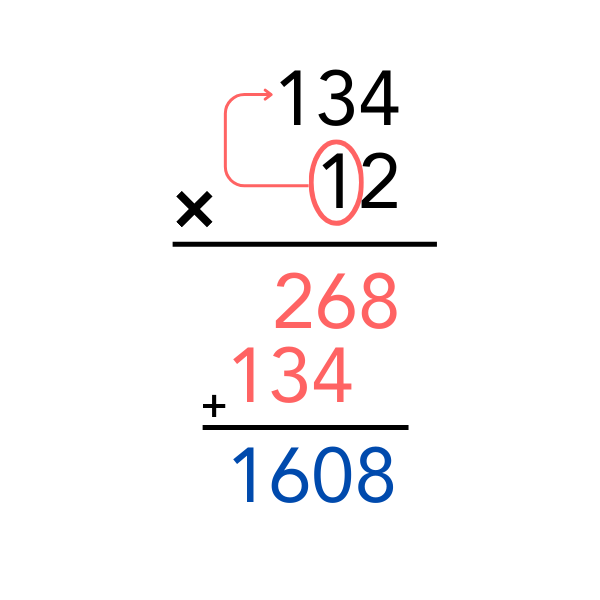
Ondalıklı Sayılarla Çarpım
Ondalıklı sayılarla çarpma yaparken, önce virgülleri geçici olarak yok sayar ve sayıları tam sayı gibi çarparsın. Ardından, sonuçta virgülü doğru yere yerleştirirsin.
Virgülün yeri belirlenirken, çarpılan iki sayının toplam ondalık basamak sayısı dikkate alınır.
Örnek:
12,3 × 3,4
- Toplam ondalık basamak sayısı: 1 + 1 = 2 (12,3'teki 3 ve 3,4'teki 4)
- Çarpma sonucu: 41,82
Biraz pratik yaptıktan sonra, ister tam sayılarla ister ondalıklı sayılarla olsun, çarpma işlemlerinin düşündüğünden çok daha kolay olduğunu göreceksin.
Yapay zekâ ile özetle















